Introduction
Hello, world! Welcome to the wonderful world of programming. This is an incredibly exciting and challenging field, full of possibilities and opportunities. We are eager to see what you will create and build during your learning journey.
When it comes to programming, it is essential to understand the importance of precision and safety in code. That's why we would like to talk about Kind, a powerful formal model checker for real-time systems. It allows you to specify desired properties for your system and automatically generates test cases to ensure that the system meets these properties. This is particularly valuable for critical projects, such as security systems, where accuracy and safety are crucial.
Programming is a constant journey of learning and personal development. Don't feel discouraged if you encounter difficulties along the way, these difficulties are part of the learning process and opportunities to grow and evolve. Remember that we are here to help you along the way, don't hesitate to ask for help if you need it.
Be prepared to work hard and face challenges, but also be prepared to celebrate your accomplishments and achievements. Remember to have fun and enjoy every moment of this incredible learning journey.
Good luck on your learning journey, and we look forward to seeing what you will create and build.
Starting
Welcome to Kind!
Kind is an efficient, minimalist, and practical language that aims to rethink functional programming from scratch with a modern and consistent design.
The goal of this documentation is to be as simple as possible to learn Kind. That's why we decided to adopt a minimalist and simple design so that you can quickly find what you need.
Quick Navigation Index
- About Kind;
- Installation guide for MacOS, Linux, and Windows;
- Command guide;
- Learning the basic concepts of Kind;
Hello, Kind!
Kind is a programming language that aims to be practical and conventional. It is statically typed, which means that data types are defined beforehand and checked at compile time. These types are powerful enough to allow the proof of mathematical theorems.
When creating a new program in Kind, you have access to a vast universe of resources and functionalities. It's like all the tools you need are already there, ready to be used. With each new function or library you discover, it's like a new part of this universe is revealed.
Just like in a real universe, there is always something new to be discovered in Kind. There is a plethora of resources and tools available for you to explore and use in your programs. With such variety, it's possible to create solutions for practically any problem you can imagine.
If you're interested in learning more about programming and exploring the vast universe of Kind, then becoming a Kind programmer can be an exciting and rewarding adventure. There are many other Kind programmers out there to collaborate and learn with, making this journey even more exciting.
In summary, Kind is a modern, powerful, and versatile programming language that offers many opportunities for those who want to learn and explore the vast universe of programming. If you're interested in becoming a Kind programmer, there are many resources available to help you get started, from official documentation to active communities of users and developers.
Installation
This guide teaches you how to download and install Kind through Rust, using "Cargo", a tool used to manage packages. It may be necessary to have an internet connection to proceed with this guide.
Firstly, install Rust using this link
- Currently, Cargo is the only way to install Kind.
- This guide was written when Kind was in beta version. Therefore, it is necessary to install the nightly version.
Installing Kind on Linux or MacOS
Use your package manager (Cargo) to install Kind. To do this, open the terminal and type the following code:
cargo +nightly install kind2
Installing Kind on Windows
For Windows users, it is possible to use Kind through CMD or WSL2. If you choose WSL, the installation method is in this link.
Use your package manager (Cargo) to install Kind. To do this, open Bash(WSL2) or Terminal(CMD) and type the following command:
cargo +nightly install kind2
Cloning the Kind Repository - Method 1
Clone the Kind repository using the git command "git clone", as follows:
git clone https://github.com/HigherOrderCO/Kind
After the cloning step, use the following command for installation:
cargo +nightly install --path crates/kind-cli --force
Cloning the Kind Repository - Method 2
Cargo allows you to install using git, without the need to clone any repository, as follows:
cargo +nightly install --git https://github.com/HigherOrderCO/kind.git
By following the above steps, we can start using Kind.
Hello World!
At this point, Kind should already be installed on your machine. If not, please go back to the installation and follow the instructions.
In this guide, we will be using command lines and text editors, so make sure your terminal is open to proceed with the steps.
Creating the Files
First of all, create a directory to store the Kind files. It is recommended to use a dedicated directory to keep all exercises and examples, but feel free to do as you please. The three commands below will create a directory named 'KindExamples' and a file named 'hello_world.kind2' inside the project directory. Use them in order:
// Linux, Mac or WSL
mkdir KindExamples
cd KindExamples
touch hello_world.kind2
The .kind2 extension is what makes it a Kind file. For example, a file that ends with .exe is an executable; .js is a JavaScript file; .rs is a Rust file, etc.
If the commands were used correctly, the hello_world.kind2 file should be inside the KindExamples folder. So let's have some fun, CODING!
Hello World
Open the hello_world.kind2 file in your text editor, it will be empty, but don't worry. From now on, there will be some advanced concepts. Everything will make sense in the future, and pertinent concepts will be explained in due time. It is recommended that you manually type the codes, instead of copying and pasting them into your file.
Let's write your first code in the hello_world.kind2 file:
Main {
"Hello, Kind!"
}
Type Checking
With the code ready, you should use Type Checking to check if everything is in order. The type checker is still unknown in this guide, but it will be explained in more detail later. For now, just understand it as a checker that verifies if the file is correctly "typed".
To check the type of a Kind file, simply use the command kind2 check fileName.kind2. For the hello_world.kind2 file, it would be:
kind2 check hello_world.kind2
The message All terms check. means your file is ready!
All terms check.
Is the type checking correct? Then let's run the code.
Running the code
To run a file in Kind, use the command kind2 run fileName.kind2. It should look like this:
kind2 run hello_world.kind2
And there you go! Your terminal should print "Hello, Kind!" back to you.
Remember to do all the steps above, check the type, and then run
Great, now that you have your first Kind program running, you can start exploring more about the language and its features. Congratulations on your progress!
If you have any questions or need help, don't hesitate to ask. We are always available to help!
Hello Kind!
Now that you have learned how to create and run a Kind file, let's dive deeper into the basics of Kind. In the next section, you will learn about Kind's type system, syntax, variables, and functions.
Kind's Type System
Kind has a static type system, which means that the type of a variable must be known at compile-time. Kind has a rich type system that includes primitive types, algebraic data types, and type parameters.
Kind Syntax
Kind's syntax is inspired by functional programming languages like Haskell. The syntax is concise and expressive, making it easy to read and write code. It uses indentation instead of braces to define blocks of code.
Variables
In Kind, variables are declared using the keyword let followed by the variable name. For example:
let x = 42
Functions
Functions in Kind are declared using the first letter capitalized. The function may take parameters or not and returns a value. For example:
Nat.add (a: Nat) (b: Nat) : Nat
This is just a brief overview of the basics of Kind. You will learn more about these concepts as you progress through the guide. Now that you have learned about Kind's basics, it's time to move on to the next section and learn about advanced concepts in Kind programming.
Basics
Introduction
The functional programming style brings programming closer to simple and everyday mathematics: If a procedure or method has no side effects, then (ignoring efficiency) all we need to understand about it is how to map inputs to outputs - in other words, we can think of it as a concrete method that computes a mathematical function. This is one sense of "functional" in "functional programming". The direct connection between programs and simple mathematical objects supports both the formality of correctness proofs and informal reasoning about program behavior.
The other sense in which functional programming is "functional" is that it emphasizes the use of functions as first-class values - that is, values that can be passed as arguments to other functions, returned as results, included in data structures, etc. The recognition that functions can be treated in this way as data enables a range of useful commands.
Other common features of functional languages include algebraic data types and pattern matching, which make it easy to construct and manipulate data structures, and sophisticated polymorphic type systems, supporting abstraction and code reuse. Kind contains all of these features.
The first half of this chapter introduces the most basic elements of the Kind functional programming language. The second half introduces some basic techniques that can be used to prove properties about programs in Kind.
Enumerated Types
An unusual aspect of Kind, similar to other proof languages such as Idris and Coq, is that its built-in toolset is quite small. For example, instead of providing the usual range of primitive types (booleans, lists, strings, etc), Kind has only two primitive types (U60: unsigned 60-bit binary integers) and (F60: unsigned 60-bit binary floating point numbers) and offers a powerful mechanism for defining new data types from scratch, from which all these familiar types and more can be derived.
To demonstrate how the definition mechanism works, let's start with a simple example.
Days of the Week
The following declaration tells Kind that we are declaring a new set of data - a Type.
type Day { // Day is a Type
monday // Monday is a Day
tuesday // Tuesday is a Day
wednesday // Wednesday is a Day
thursday // Thursday is a Day
friday // Friday is a Day
saturday // Saturday is a Day
sunday // Sunday is a Day
}The type is called Day, and its members are Monday, Tuesday, Wednesday, etc. The <name> : <type> definition can be read as "name is a type".
Above, we have both an example of creating a new Day : Type, and declaring an element of an existing type Wednesday : Day.
Now that we have defined what a Day is, we can write functions that operate using this type. Type the following:
NextWeekday (d: Day) : DayThis declares that we have a function called NextWeekday, which takes an argument called d, of type Day, and returns a Day. Continue defining the function as follows:
NextWeekday Day.monday = ?
NextWeekday Day.tuesday = ?
NextWeekday Day.wednesday = ?
NextWeekday Day.thursday = ?
NextWeekday Day.friday = ?
NextWeekday Day.saturday = ?
NextWeekday Day.sunday = ?Here, we are doing what we call pattern matching. We are declaring how the function should run for each possibility of the input d. It won't always be necessary to do this, as will be shown in examples later on.
Finally, complete the functions by writing what each one should return, and use spaces to style as you prefer:
NextWeekday Day.monday = Day.tuesday
NextWeekday Day.tuesday = Day.quarta
NextWeekday Day.wednesday = Day.thursday
NextWeekday Day.thursday = Day.sexta
NextWeekday Day.friday = Day.monday
NextWeekday Day.saturday = Day.monday
NextWeekday Day.sunday = Day.mondayWith the function finished, we can check its operation with some examples. The main way to do this in Kind is to create a Main function in your file and run it with the command kind2 run <file>.
For example, if you write the following Main and run the file:
Main {
// Two workdays after Saturday
NextWeekday (NextWeekday Day.saturday)
}You should get something like:
(Day.tuesday)
Another way to test your code is to say what we expect the code to return, through a proof:
// // The third workday after a Monday is a Thursday
TestNextWeekday : Prop.Equal Day (NextWeekday (NextWeekday (NextWeekday Day.monday))) Day.thursday
TestNextWeekday = Prop.Equal.reflThe details of how proofs work will be explained later on. For now, what needs to be understood is:
- We have the realization that
(NextWeekday (NextWeekday (NextWeekday Day.monday)))is equal toDay.thursday - This realization was named
TestNextWeekday TestNextWeekday = Equal.reflsays that the realization can be proven using only simplification on both sides.
To test that this proof (and any other proof going forward) is correct, you need to check the file using the command kind2 check <file>, which should return something like:
All terms check.
Booleans
Similarly, we can declare the Bool type for booleans:
type Bool {
true
false
}We are declaring our own booleans just to demonstrate how to do everything from scratch. Kind has its own default implementation of booleans in the standard package (Wikind), along with many other structures and proofs.
In fact, at the time of writing, you need to be working within the Wikind folder to do proofs and the theorem resolution utilities are not built-in.
Functions that operate on booleans are defined in the same way as seen earlier:
// Logic NOT
Notb (b: Bool) : Bool
Notb Bool.true = Bool.false
Notb Bool.false = Bool.true
// Logic AND
Andb (b1: Bool) (b2: Bool) : Bool
Andb Bool.true b2 = b2
Andb Bool.false b2 = Bool.false
// Logic OR
Orb (b1: Bool) (b2: Bool) : Bool
Orb Bool.true b2 = Bool.true
Orb Bool.false b2 = b2The last two functions demonstrate the syntax of Kind for multi-argument functions, and also show that it is possible to pattern match only on some of the variables of the function, not necessarily all.
The cases of the last function can be exhaustively tested (all possibilities) as shown below, creating the truth table of the logical operation.
TestOrb1 : Prop.Equal Bool (Orb Bool.true Bool.false) Bool.true
TestOrb1 = Prop.Equal.refl
TestOrb2 : Prop.Equal Bool (Orb Bool.false Bool.false) Bool.false
TestOrb2 = Prop.Equal.refl
TestOrb3 : Prop.Equal Bool (Orb Bool.false Bool.true) Bool.true
TestOrb3 = Prop.Equal.refl
TestOrb4 : Prop.Equal Bool (Orb Bool.true Bool.true) Bool.true
TestOrb4 = Prop.Equal.reflNandb
Replace the hole "?", completing the following function;
then check if it is correct using the following statements (Analogous to how it was done for the Orb function). The function returns Bool.true if any of its inputs is Bool.false.
Nandb (b1: Bool) (b2: Bool) : Bool
Nandb b1 b2 = ?
Test_nandb1 : Prop.Equal Bool (Nandb Bool.true Bool.false) Bool.true
Test_nandb1 = ?
Test_nandb2 : Prop.Equal Bool (Nandb Bool.false Bool.false) Bool.true
Test_nandb2 = ?
Test_nandb3 : Prop.Equal Bool (Nandb Bool.false Bool.true) Bool.true
Test_nandb3 = ?
Test_nandb4 : Prop.Equal Bool (Nandb Bool.true Bool.true) Bool.false
Test_nandb4 = ?And3
Do the same for the Andb3 function below. This function should return Bool.true if all inputs are Bool.true, and Bool.false otherwise.
Andb3 (b1: Bool) (b2: Bool) (b3: Bool) : Bool
Andb3 b1 b2 b3 = ?
Test_andb3_1 Prop.Equal Bool (Andb3 Bool.true Bool.true Bool.true) Bool.true
Test_andb3_1 = ?
Test_andb3_2 Prop.Equal Bool (Andb3 Bool.false Bool.true Bool.true) Bool.false
Test_andb3_2 = ?
Test_andb3_3 Prop.Equal Bool (Andb3 Bool.true Bool.false Bool.true) Bool.false
Test_andb3_3 = ?
Test_andb3_4 Prop.Equal Bool (Andb3 Bool.true Bool.true Bool.false) Bool.false
Test_andb3_4 = ?Types of functions
All expressions in Kind have a type, describing what type of thing it computes.
For example, Bool.true has type Bool, just like Notb Bool.true also has type Bool.
Functions like Notb, before they receive arguments, also have a type, just like Bool.true or Bool.false.
Their types are called Function Types, and are denoted with arrows.
Notb, for example, would be denoted as Bool -> Bool, which can be read as
"a function that takes a Bool as input and returns a value of type Bool".
Similarly, the type of the Andb function is Bool -> Bool -> Bool, meaning
"a function that takes two arguments of type Bool and returns a value of type Bool".
Modules
We don't have a module system yet :pensive:. To use functions from other files, you need to create a file within the same directory (e.g., the root folder of Kindex).
Use
The use statement is a useful feature in the Kind language that allows you to create aliases for functions or data types. It simplifies the usage of specific functions or types in your code. Let's explore its usage with practical examples.
Step 1: Importing Functions with use
The first use of use is to import functions. Suppose you are working with the Data.Nat.succ function and want to import it with a shorter alias, such as Succ, for easier usage in your code. Here's an example:
#![allow(unused)] fn main() { use Data.Nat as Succ }
With this statement, you import the Data.Nat.succ function and associate it with the Succ alias. You can now use Succ instead of Data.Nat.succ to refer to that function.
Step 2: Using Aliases for Data Types
In addition to importing functions, use can also create aliases for specific data types. Suppose you want to create an alias for the Data.Nat type called Nat. Here's an example:
#![allow(unused)] fn main() { use Data.Nat as Nat }
With this statement, you import the Data.Nat type and associate it with the Nat/ alias. You can now use Nat/ to refer to the Nat data type.
Now, let's use the Nat/ alias in a function called Succ:
#![allow(unused)] fn main() { Succ (n: Nat/) : Nat/ Succ n = Nat/succ n }
The Succ function takes a parameter n of type Nat/ and returns a value of the same type . Within the function body, we use the Nat/ alias to invoke the succ function associated with the Nat.
Step 3: Using Aliases in Other Functions
Next, let's explore how aliases can be used in other functions. Consider the Is_equal function, which compares two Bool/ values and returns a Bool/ result:
#![allow(unused)] fn main() { Is_equal (b1: Bool/) (b2: Bool/) : Bool/ Is_equal b1 b2 = match Bool/ b1 { true => b2 false => match b2 { true => Bool/false false => Bool/true } } }
In this example, we use the Bool/ alias to refer to the Data.Bool type within the match pattern. This makes the code more readable and avoids unnecessary repetition of the full module name.
Step 4: Explaining Aliases with an Additional Example
To further illustrate the use of aliases, let's consider the Add_zero function, which proves that adding zero to a number n results in n using the Equal for propositional equality:
#![allow(unused)] fn main() { Add_zero (n: Nat/) : Equal/ (Nat/add 0n n) n Add_zero n = Equal/refl }
In this function, we use the Equal/ alias to refer to the Prop.Equal type, which handles propositional equality. With the alias, we declare that the return type of the function is a proof of equality between the expression (Nat/add 0n n) and n. We also use the Equal/refl alias to create a reflexive proof of equality.
Conclusion
The use statement is a powerful tool in the Kind language that allows you to create aliases for functions or data types. It simplifies the usage of functions and types, making the code more readable and concise. With use, you can import functions with shorter aliases and create aliases for specific data types. I hope this tutorial has helped you understand the usage of use in Kind.
Numbers
The types we have defined so far are examples of enumerated types: their definitions explicitly enumerate a finite set of elements. A more interesting way to define a type is to establish a collection of inductive rules describing its elements. For example, we can define natural numbers as follows:
type Nat {
zero
succ (pred: Nat)
}This definition can be read as:
Nat.zerois a natural number;Nat.succis a constructor that takes a natural number, constructing another natural number;- That is, if
nis a natural number, then(Nat.succ n)will also be.
- That is, if
Every type defined inductively (such as Nat, Bool ou Day) is a set of expressions. The definition of Nat says how expressions of type Nat can be constructed:
- The expression
Nat.zerobelongs to the set ofNat; - If
nis an expression in the set ofNat, then(Nat.succ n)is also an expression in the set ofNat; - Expressions formed in these two ways are the only ones that belong to
Nat.
The same rules apply to our definitions of Day and Bool.
The annotations we used for them are analogous to the Nat.zero constructor, indicating that they do not receive any arguments.
These three conditions demonstrate the power of inductive declarations. They imply that the expression Nat.zero, the expression (Nat.succ Nat.zero), the expression (Nat.succ (Nat.succ Nat.zero)) and so on, are of the Nat set, while other expressions such as Bool.true, (Andb Bool.true Bool.false), and (Nat.succ (Nat.succ Bool.false)) are not.
We can write simple functions using pattern matching on natural numbers in the same way we did above - for example, the predecessor function:
Pred (n: Nat) : Nat
// Since natural numbers are strictly non-negative,
// we use as a convention that anything that would be
// less than 0 returns 0
Pred Nat.zero = Nat.zero
Pred (Nat.succ k) = kThe second pattern can be read as: "if n has the form (Nat.succ k) for some k, return k."
MinusTwo (n: Nat) : Nat
MinusTwo Nat.zero = Nat.zero
MinusTwo (Nat.succ Nat.zero) = Nat.zero
MinusTwo (Nat.succ (Nat.succ k)) = kTo avoid having to write a sequence of Nat.succ every time you want a Nat, you can use the n suffix at the end of any number, for example o 5n, which takes a number written in the primitive type U60 plus the n suffix and returns the corresponding Nat.
{...}
Test : Equal/ Nat 6n (Nat.succ (Nat.succ (Nat.succ (Nat.succ (Nat.succ (Nat.succ Nat.zero))))))
Test = Equal/reflThe Nat.succ constructor has type Nat -> Nat, as do the functions MinusTwo and Pred. They are all things that, when applied to a Nat, return a Nat. The essential difference between Nat.succ and the other two, however, is that functions come with reduction rules - for example, Pred (Nat.succ Nat.zero) is reducible to Nat.zero - while Nat.succ does not. Although it is a function applicable to an argument, it does not compute anything.
For most number function definitions, pattern matching alone is not enough: we will also need recursion. For example, to check whether a number n is even, we can recursively check whether n-2 is even.
Evenb (n: Nat) : Bool/
Evenb Nat.zero = Bool/true
Evenb (Nat.succ Nat.zero) = Bool/false
Evenb (Nat.succ (Nat.succ k)) = Evenb kWe can define Oddb (a function to check if a number is odd) with a similar recursive declaration, but we also have a simpler and somewhat easier to work with definition:
Oddb (n: Nat) : Bool/
Oddb n = Notb (Evenb n)TestOddb1 : Equal/ Bool/ (Oddb 1n) Bool/true
TestOddb1 = Equal/refl
TestOddb2 : Equal/ Bool/ (Oddb 4n) Bool/false
TestOddb2 = Equal/reflNaturally, we can also define functions with multiple arguments by recursion.
Plus (n: Nat) (m: Nat) : Nat
Plus Nat.zero m = m
Plus (Nat.succ k) m = Nat.succ (Plus k m)Adding 3n and 2n will return 5n as expected.
The simplification that Kind performs to arrive at this value can be visualized as follows:
Plus (Nat.succ (Nat.succ (Nat.succ Nat.zero))) (Nat.succ (Nat.succ Nat.zero))
> Nat.succ (Plus (Nat.succ (Nat.succ Nat.zero)) (Nat.succ (Nat.succ Nat.zero)))
by the second rule of Plus
> Nat.succ (Nat.succ (Plus (Nat.succ Nat.zero)) (Nat.succ (Nat.succ Nat.zero)))
by the second rule of Plus
> Nat.succ (Nat.succ (Nat.succ (Plus Nat.zero (Nat.succ (Nat.succ Nat.zero)))))
by the second rule of Plus
> Nat.succ (Nat.succ (Nat.succ (Nat.succ (Nat.succ Nat.zero))))
by the first rule of Plus
Multiplication can be defined using the definition of Plus, as follows:
Mult (n: Nat) (m: Nat) : Nat
Mult Nat.zero m = Nat.zero
Mult (Nat.succ k) m = Plus m (Mult k m)TestMult1 : Equal/ Nat (Mult 3n 3n) 9n
TestMult1 = Equal/reflYou can also use pattern matching on two expressions at the same time:
Minus (n: Nat) (m: Nat) : Nat
Minus Nat.zero m = Nat.zero
Minus n Nat.zero = n
Minus (Nat.succ k) (Nat.succ j) = Minus k jThe Exp function can be defined using Mult (analogous to how Mult is defined using Plus):
Exp (base: Nat) (power: Nat) : Nat
Exp base Nat.zero = Nat.succ Nat.zero
Exp base (Nat.succ k) = Mult base (Exp base k)Factorial
Recall the basic mathematical definition of factorial:
\[\mathrm
Factorial(n) = \begin{cases}
\text{if $n$} = 0\,& 1 \
\\ \text{else} & n * Factorial(n-1)
\end{cases}
\]
\[ f(x)=\begin{cases}x&(x = 1)\\x f(x-1)&(x\gt 1)\end{cases} , x\in \Bbb{N} \]
Translate the factorial function into Kind2:
Factorial (n: Nat) : Nat
Factorial n = ?TestFactorial1 : Equal/ Nat (Factorial 3n ) 6n
TestFactorial1 = ?
TestFactorial2 : Equal/ Nat (Factorial 5n) 120n
TestFactorial2 = ?The Eql function tests equality between Naturals, returning a boolean.
Eql (n: Nat) (m: Nat) : Bool/
Eql Nat.zero Nat.zero = Bool/true
Eql Nat.zero (Nat.succ j) = Bool/false
Eql (Nat.succ k) Nat.zero = Bool/false
Eql (Nat.succ k) (Nat.succ j) = Eql k jTheLte function tests if the first argument is less than or equal to the second, returning a boolean.
Lte (n: Nat) (m: Nat) : Bool/
Lte Nat.zero m = Bool/true
Lte (Nat.succ k) Nat.zero = Bool/false
Lte (Nat.succ k) (Nat.succ j) = Lte k jTestLte1 : Equal/ Bool/ (Lte 2n 2n) Bool/true
TestLte1 = Equal/refl
TestLte2 : Equal/ Bool/ (Lte 2n 4n) Bool/true
TestLte2 = Equal/refl
TestLte3 : Equal/ Bool/ (Lte 4n 2n) Bool/false
TestLte3 = Equal/reflBlt_nat
The Blt_natfunction tests the "less than" relationship in natural numbers.
Instead of creating a new recursive function, define it using previously defined functions.
Blt_nat (n: Nat) (m: Nat) : Bool/
Blt_nat n m = ?Test_blt_nat_1 : Equal/ Bool/ (Blt_nat 2n 2n) Bool/false
Test_blt_nat_1 = ?
Test_blt_nat_2 : Equal/ Bool/ (Blt_nat 2n 4n) Bool/true
Test_blt_nat_2 = ?
Test_blt_nat_3 : Equal/ Bool/ (Blt_nat 4n 2n) Bool/false
Test_blt_nat_3 = ?Proof by Simplification
Now that we have defined some data types and functions, let's start proving properties of their behaviors. In fact, we have already been doing this: each function in the previous sections that starts with Test makes a precise assertion about the behavior of some function for specific inputs. The proofs of these assertions were always the same: use Equal.refl to check that both sides are indeed identical.
The same type of "proof by simplification" can be used to prove more interesting properties. For example, the fact that Nat.zero is a "neutral element" on the left-hand side of addition can be proven simply by observing that Plus Nat.zero n reduces to n, regardless of what n is, a fact that can be read directly from the definition of Plus.
Plus_Z_n (n: Nat) : Equal/ Nat (Plus Nat.zero n) n
Plus_Z_n n = Equal/reflOther similar theorems can be proven in a similar way.
Plus_1_l (n: Nat) : Equal/ Nat (Plus (Nat.succ Nat.zero) n) (Nat.succ n)
Plus_1_l n = Equal/refl
Mult_0_l (n: Nat) : Equal/ Nat (Mult Nat.zero n) Nat.zero
Mult_0_l n = Equal/refl The _l indicates that the proof involves the value on the left-hand side. For example: the proof of adding 1 on the left-hand side (Plus_1_l) or the proof of multiplying by zero on the left-hand side (Mult_0_l).
Although simplification is powerful enough to prove some general facts, there are several statements that cannot be demonstrated with simplification alone. For example, we cannot use it to prove that Nat.zero is a neutral element for addition on the right-hand side.
Plus_n_Z (n: Nat) : Equal/ Nat n (Plus n Nat.zero)
Plus_n_Z n = Equal/refl- ERROR Type mismatch
• Got : Equal Nat n n
• Expected : Equal Nat n (Plus n 0n)
• Context:
• n : Nat
Plus_n_Z n = Equal.refl
┬─────────
└Here!
(Can you explain why this is?)
The next chapter will introduce the concept of induction, a powerful technique that can be used to demonstrate this theorem. For now, however, let's see some more simple types of proof.
Proof by Application
Our first tool for proving non-trivial theorems will be applying functions to both sides of an equality. For this, we will use the function Equal.apply, which takes an equality (Equal) and a function, and applies this function to both sides of the equality, generating a new equality.
For example:
Example_apply (n: Nat) (m: Nat) (e: Equal/ Nat m n) : Equal/ Nat (Nat.succ m) (Nat.succ n)
Example_apply n m e = ?What do we have here? We have a proof that takes another proof/equality as argument. This means that we will carry out our proof assuming that the proof given as argument is also true. So, reading the statement of the proof, we have: "Given two naturals, m and n, and a proof that they are equal, prove that Nat.succ m and Nat.succ n are also equal".
We learned in our math classes that applying a function to both sides of an equality preserves the equality (x/2 = 3 -> 2x/2 = 23), and we can see that to prove what we want, we need to apply the function Nat.succ to both sides of e, using Equal.apply.
+ INFO Inspection.
• Expected: (Equal Nat (Nat.succ m) (Nat.succ n))
• Context:
• n : Nat
• m : Nat
• e : (Equal Nat m n)
Example_apply n m e = ?
┬
└Here!
How does Equal.apply work: It takes as first argument the function to be applied to both sides, and as second argument the equality to which to apply the function. If you didn't understand the passage of the argument function (x => Nat.succ x), it is what we call a lambda function, and is also known as an anonymous function. Lambda functions are identified by their arrow =>, where on the left side of the arrow is the name of the function argument - use any name you want - and on the right side is the body of the function: what it returns. Our current lambda function is a function that takes any x and returns Nat.succ x.
We can see the result of this by check the file:
+ INFO Inspection.
• Expected: (Equal Nat (Nat.succ m) (Nat.succ n))
• Context:
• n : Nat
• m : Nat
• e : (Equal Nat m n)
• e_apply : (Equal Nat (Nat.succ m) (Nat.succ n))
• e_apply = (Equal.apply Nat Nat m n (x => (Nat.succ x)) e)
let e_apply = Equal.apply (x => Nat.succ x) e
?
┬
└Here!
As e_apply is an equality of type Equal/ Nat (Nat.succ m) (Nat.succ n), the proof we are looking for is simply to return it, and we will have concluded our proof.
Example_apply (n: Nat) (m: Nat) (e: Equal/ Nat m n) : Equal/ Nat (Nat.succ m) (Nat.succ n)
Example_apply n m e =
let e_apply = Equal/apply (x => Nat.succ x) e
e_apply All terms checked.
Proof by Case Analysis
The next tool for formal proofs will be case analysis, which means using pattern matching in the proof. For example, let's prove that the logical AND of anything and False is always False:
Example_case_analysis (b: Bool/) : Equal/ Bool/ (Andb b1 Bool/false) Bool/false
Example_case_analysis b = ?Although it may seem like a proof that could be solved simply with Equal/refl, it's not the case. This is because the Andb function pattern matches on the first argument, and we don't have its value in the proof, so it remains "stuck".
To give a value to it and show that the proof is correct for both Bool values, we pattern match in the proof, creating two different proofs: one for when b is Bool/true and one for when it's Bool/false.
Example_case_analysis (b: Bool/) : Equal/ Bool/ (Andb b Bool/false) Bool/false
Example_case_analysis Bool/true = ?
Example_case_analysis Bool/false = ?And both of these proofs are directly solvable with Equal/refl, since the type checker can reduce both of them to Equal Bool.false Bool.false directly.
Example_case_analysis (b: Bool/) : Equal/ Bool/ (Andb b Bool/false) Bool/false
Example_case_analysis Bool/true = Equal/refl
Example_case_analysis Bool/false = Equal/reflProof by Rewriting
This theorem is a bit more interesting than the previous ones:
Plus_id_example (n: Nat) (m: Nat) (e: Equal/ Nat n m) : Equal/ Nat (Plus n n) (Plus m m)As shown before, this is a proof that has another proof or hypothesis within its arguments: in this case, we have Equal n m - meaning, n and m are equal.
Since n and m are arbitrary numbers, we can't just use simplification to prove the theorem. Instead, we observe that, since we assume Equal n m, we could substitute n for m in the goal and both sides will be equal. The function we use to perform this substitution is Equal.rewrite.
Since we can't rewrite directly in the goal, we use another equality and make it equal to the goal. In our case, we will use an Equal.apply on e to obtain this equality.
Plus_id_example (n: Nat) (m: Nat) (e: Equal/ Nat n m) : Equal/ Nat (Plus n n) (Plus m m)
Plus_id_example n m e =
let app = Equal/apply (k => Plus k n) e
? + INFO Inspection.
• Expected: Equal Nat (Plus n n) (Plus m m)
• Context:
• n : Nat
• m : Nat
• e : Equal Nat n m
• app : Equal Nat (Plus n n) (Plus m n)
• app = Equal.apply Nat Nat n m (k => (Plus k n)) e
let app = Equal.apply (k => Plus k n) e
?
┬
└Here!
This app will be of type Equal (Plus n n) (Plus m n), as shown in the comment. With this done, we need to replace n with m on the right-hand side of the equality, and for that we use rewrite:
Plus_id_example (n: Nat) (m: Nat) (e: Equal/ Nat n m) : Equal/ Nat (Plus n n) (Plus m m)
Plus_id_example n m e =
let app = Equal/apply (k => Plus k n) e
let rrt = Equal/rewrite e (x => Equal/ (Plus n n) (Plus m x)) app
rrt+ INFO Inspection.
• Expected: Equal Nat (Plus n n) (Plus m m)
• Context:
• n : Nat
• m : Nat
• e : Equal Nat n m
• app : Equal Nat (Plus n n) (Plus m n)
• app = Equal.apply Nat Nat n m (k => (Plus k n)) e
• rrt : Equal Nat (Plus n n) (Plus m m)
• rrt = Equal.rewrite Nat n m e (x => Equal Nat (Plus n n) (Plus m x)) app
The return value of the Equal.rewrite operation will be the proof we need, so we just return the result directly from the function.
Plus_id_exercise
Prove that:
Plus_id_exercise (n: Nat) (m: Nat) (o: Nat) (e1: Equal/ Nat n m) (e2: Equal/ Nat m o) : Equal/ Nat (Plus n m) (Plus m o)
Plus_id_exercise n m o e1 e2 = ?Equal.chain and Equal.mirror
In this section we will not discuss any inherently new tool, but rather some proof utilities to make use of the previous tools easier.
Consider the example:
Example_mirror (a: Nat) (b: Nat) (e: Equal/ Nat a b) : Equal/ Nat b aIt seems like a trivial example. If a is equal to b, then b is equal to a, right? Although correct, the type checker of Kind does not recognize this equality, because for it, the order is important. For such situations, we have the function Equal/mirror, which simply swaps the sides of an equality.
Example_mirror (a: Nat) (b: Nat) (e: Equal/ Nat a b) : Equal/ Nat b a
Example_mirror a b e =
let mir = Equal/mirror e
mir+ INFO Inspection.
• Expected: Equal Nat b a
• Context:
• a : Nat
• b : Nat
• e : Equal Nat a b
• mir : Equal Nat b a
• mir = Equal.mirror Nat a b e
Although it may not seem very useful at the moment, this operation is very useful for our second utility: Equal/chain. Equal/chain is a specific case of Equal/rewrite, in which you rewrite an entire side of an equality using another.
Example_chain (a: Nat) (b: Nat) (c: Nat) (e1: Equal/ Nat b (Plus a a)) (e2 : Equal/ Nat c (Plus a a)) : Equal/ Nat b cSince we already know Equal.rewrite, we could use it to solve this theorem, but instead we will use Equal.chain.Equal.chain works by "chaining" two equalities that have the same expression on the right side of the first equality and on the left side of the second, "gluing" these equalities together by the common expression, generating a new equality with the other two expressions (Equal.chain (a = b) (b = c) = (a = c)). For example, in our example, the right side of the two equalities is equal. If we use Equal.mirror on one of them, we can then use Equal.chain on them:
Example_chain (a: Nat) (b: Nat) (c: Nat) (e1: Equal/ Nat b (Plus a a)) (e2 : Equal/ Nat c (Plus a a)) : Equal/ Nat b c
Example_chain a b c e1 e2 =
let e3 = Equal/mirror e2
let chn = Equal/chain e1 e3
+ INFO Inspection.
• Expected: Equal Nat b c
• Context:
• a : Nat
• b : Nat
• c : Nat
• e1 : Equal Nat b (Plus a a)
• e2 : Equal Nat c (Plus a a)
• e3 : Equal Nat (Plus a a) c
• e3 = Equal.mirror Nat c (Plus a a) e2
• chn : Equal Nat b c
• chn = Equal.chain Nat b (Plus a a) c e1 e3
More Exercises
Boolean_functions
Use the knowledge taught so far to solve the theorem:
Identity_fn_applied_twice (f: Bool/ -> Bool/) (e: (x: Bool/) -> Equal/ Bool/ (f x) x) (b : Bool/) : Equal/ Bool/ (f (f b)) b
Identity_fn_applied_twice f e b = ?Then, solve the negation_fn_applied_twice theorem, which is the same as the previous one, but changing the hypothesis to Equal (f x) (Not x)
Andb_eq_orb
Prove the following theorem (Remember that you can prove intermediate theorems separately):
Andb_eq_orb (b: Bool/) (c: Bool/) (e: Equal/ Bool/ (Andb b c) (Orb b c)) : Equal/ Bool/ b c
Andb_eq_orb b c prf = ?Binary
Consider a different representation of natural numbers using a binary system instead of unary. That is, instead of having only zero or one successor of a number, we can have:
- zero;
- twice a number;
- twice a number plus 1.
- First, write an inductive definition of this type, calling it
Bin. (Remember that, in essence, the definition ofNataszeroorsucc nhas no intrinsic meaning. It only says that an element ofNatcan be azeroor asucc nifnis alsoNat. The interpretation of this as a system of values 0, 1, 2, etc., comes from how we work with this typeNat. Your definition ofBinideally will be as simple as well. It will be the functions you make onBinthat will give mathematical sense to it). - Then write an
Incrfunction to increment aBin, and aBin_to_natfunction to convert fromBintoNat. - Write five proofs that test your increment and conversion functions. Note that incrementing a binary and then converting it should result in the same result as converting it first and then incrementing the
Nat.
Induction: Proof by Induction
Induction
In this chapter, we will learn about proof by induction. Before we move on to induction itself, we can analyze simple cases where the reflection of the case already proves the theorem.
Problems.t0 (n: Nat/) : Equal/ Nat/ (Plus Nat/zero n) nWhen checking the theorem statement, we receive the following response:
+ INFO Inspection.
• Expected: (Equal Nat n n)
• Context:
• n : Nat
Problems.t0 n = ?
┬
└Here!
In Problems.t0, Kind automatically reduces the sum of 0 + n to n, and we need to prove the equality between n and n. In this case, we simply write Equal/refl and we get the confirmation response:
All terms check.
Problems.t1 (n: Nat/) : Equal/ Nat/ (Plus n Nat/zero) nAfter solving the first problem, the next one is very similar, it is the sum of n + 0 = n and this similarity may lead us to believe that invoking the reflection is enough. However, in the first case, Kind automatically reduces and in this one, we get the following response:
+ INFO Inspection.
• Expected: (Equal Nat (Plus n 0n) n)
• Context:
• n : Nat
Problems.t1 n = ?
┬
└Here!
In the first case, Kind reduces because zero is on the right side and the Type Checker automatically reduces the sum between 0 and n to n. However, when the first input is a variable, Kind needs to check for each case and as it is a natural number, there are infinitely many cases to be tested, that is, from zero to infinity.
At first, we may think that there are so many cases and it is impossible to analyze all of them, as there are infinitely many, but soon we realize that it is possible to reduce them to two, one is the number zero and the other is a number that succeeds zero n times after.
Analyzing the case of zero, our goal is to prove that zero is equal to zero:
• Expected: Prop.Equal Data.Nat Data.Nat.zero Data.Nat.zeroNow, we just need to give the Equal/refl and the zero case has been proven, we just need to respond to the successor of zero.
Our goal is to prove that for every number n, adding 0 will result in n, but we already have a new tool that helps us in this proof and it is the proof for the zero case, we just need to reduce n until the only thing needed is reflection, and we can do this by recursion and to do that we define the new n as its predecessor. In Kind, we can simply do this by defining the current n as the successor of the next n and recursively calling the function for n. This is done as follows:
Problems.t1 (Nat/succ n) = ?and our new goal is to prove that the successor of the sum between n and 0 is equal to the successor of n.
- Expected: Prop.Equal Data.Nat (Data.Nat.succ (Plus n Data.Nat.zero)) (Data.Nat.succ n)To work with induction in this recursion, we must define a variable for the original case of n.
Problems.t1 (n: Nat/) : Equal/ (Plus n Nat/zero) n
Problems.t1 Nat/zero = Equal/refl
Problems.t1 (Nat/succ n) =
let ind = Problems.t1 n
?When we give the Type Check, we get the following response:
+ INFO Inspection.
• Expected: (Equal Nat (Nat.succ (Plus n 0n)) (Nat.succ n))
• Context:
• n : Nat
• ind : (Equal Nat (Plus n 0n) n)
• ind = (Problems.t1 n)
let ind = Problems.t1 n
?
┬
└Here!
When analyzing our goal and induction, we realize that the only difference between the goal and our variable ind is the Nat.succ. Therefore, we just need to increment the ind variable with Nat.succ. To do this, we create a new variable and use a lambda function:
let app = Equal/apply (x => (Nat/succ x)) indIn the above case, we call the Equal/apply function to apply our lambda function to ind. The x => (Nat/succ x) function serves to add Nat/succ to every element received in the variable. Since our ind variable is a function that takes another variable n, our lambda function increments n with Nat/succ, which returns exactly our goal:
+ INFO Inspection.
• Expected: (Equal Nat (Nat.succ (Plus n 0n)) (Nat.succ n))
• Context:
• n : Nat
• ind : (Equal Nat (Plus n 0n) n)
• ind = (Problems.t1 n)
• app : (Equal Nat (Nat.succ (Plus n 0n)) (Nat.succ n))
• app = (Equal.apply Nat Nat (Plus n 0n) n (x => (Nat.succ x)) ind)
let app = Equal.apply (x => (Nat.succ x)) ind
?
┬
└Here!
We can see that the app is exactly the same as the Expected, which is our goal, and we just need to return it, the app, for the Type Check to validate our proof:
All terms check.
There are cases where induction is even simpler - all we need to do is understand what is happening. Let's say we want to prove that a number n minus itself is always equal to zero, regardless of what that number is. How would we do it?
First, we check the case where n is zero, and it is a true equality - zero minus zero is equal to zero. Then, we induct the case to the case of zero, which we know is true. Seems complicated? It's not - it's ridiculously simple. Let's see how it looks in Kind:
Minus_diag (n: Nat/) : Equal/ Nat/ (Minus n n) Nat/zero
Minus_diag Nat/zero = Equal/refl
Minus_diag (Nat/succ n) = Minus_diag n
Notice, this is a simple induction - we say the proof holds for the number and its predecessor, and through recursion, for all predecessors up to zero, which we verified to be true.
In other words, we prove, in just three lines, that a natural number minus itself will always result in zero, regardless of what that number is.
Exercises
Prove the following using induction. You may need previously proven results.
Mult_0_r (n: Nat/) : Equal/ Nat/ (Mult n Nat/zero) Nat/zero
Mult_0_r n = ?
Plus_n_sm (n: Nat/) (m: Nat/) : Equal/ Nat/ (Nat/succ (Plus n m)) (Plus n (Nat/succ m))
Plus_n_sm n m = ?
Plus_comm (n: Nat/) (m: Nat/) : Equal/ Nat/ (Plus n m) (Plus m n)
Plus_comm n m = ?
Add_0_r (n: Nat/) : Equal/ Nat/ (Plus n Nat/zero) n
Add_0_r n = ?
Plus_assoc (n: Nat/) (m: Nat/) (p: Nat/) : Equal/ Nat/ (Plus n (Plus m p)) (Plus (Plus n m) p)
Plus_assoc n m p = ?Consider the following function that doubles its input.
Double (n: Nat/) : Nat/
Double Nat/zero = Nat/zero
Double (Nat/succ n) = Nat/succ (Nat/succ (Double n))Use induction to prove the following theorems about Double:
Double_plus (n: Nat/) : Equal/ Nat/ (Double n) (Plus n n)
Double_plus n = ?Some theorems require analyzing the best way to prove them, for example, to prove that a number is even, we could prove it for its successor, but that would require us to prove it for the successor of the successor, making the proof of Evenb more difficult by induction. So it's important to realize when it is necessary and when it is not.
Evenb_s (n: Nat/) : Equal/ Bool/ (Evenb (Nat/succ n)) (Notb (Evenb n))
Evenb_s n = ?Another case
Let's verify if the equality n +(m + 1) = 1 + (n + m) is true.
First, our problem:
Problems.t2 (n: Nat/) (m: Nat/) : Equal/ Nat/ (Plus n (Nat/succ m)) (Nat/succ (Plus n m))We verify the base case, when n is zero:
Problems.t2 Nat/zero m = Equal/refland move on to the next case
Problems.t2 (Nat/succ n) m = ?and our current goal becomes:
• Expected: Prop.Equal Data.Nat (Data.Nat.succ (Plus n (Data.Nat.succ m))) (Data.Nat.succ (Data.Nat.succ (Plus n m)))Translating, the successor of the addition of n and the successor of m is equal to the successor of the successor of the addition of n and m. To solve this problem, we will invoke induction:
let ind = Problems.t2 n mand our current goal is to prove that:
• Expected: Prop.Equal Data.Nat (Data.Nat.succ (Plus n (Data.Nat.succ m))) (Data.Nat.succ (Data.Nat.succ (Plus n m)))Again, translating, that the successor of the addition of n and the successor of m is equal to the successor of the successor of the addition of n and m.
But now we have a very useful tool, our variable ind which is:
Equal/ Nat/ (Plus n (Nat/succ m)) (Nat/succ (Plus n m))Now, analyzing our goal and our variable ind, we can see that it is enough to add Nat.succ to both sides of the induction, and it will be exactly the same as our goal. To do this, we will use a lambda function:
let app = Equal/apply (x => (Nat/succ x)) indAnd our variable app will return our goal:
Equal/ Nat/ (Nat/succ (Plus n (Nat/succ m))) (Nat/succ (Nat/succ (Plus n m)))Just return app and Kind will give us the coveted All terms check.
Using other theorems
In Kind, as in informal mathematics, large proofs are often divided into a sequence of theorems, with later proofs referring to earlier theorems. But sometimes a proof will require some varied fact that is too trivial and of too little general interest to give it its own higher-level name. In these cases, it is convenient to be able to simply state and prove the necessary "sub-theorem" exactly at the point where it is used.
Let's analyze the following addition commutation theorem:
Problems.t3 (n: Nat/) (m: Nat/) : Equal/ Nat/ (Plus n m) (Plus m n)In the first case, for n and m equal to zero we have a reflection:
Problems.t3 Nat/zero Nat/zero = Equal/reflSo we move on to the next case:
Problems.t3 (Nat/succ n) m = ?And here it seems that we have a new problem:
Expected: Prop.Equal Data.Nat (Data.Nat.succ (Plus n m)) (Plus m (Data.Nat.succ n))
Analyzing the problem, we realize that there is a theorem already proven within it, that the successor of the addition of two numbers is equal to the addition of one number with its successor, so we can use that to our advantage.
We will start by applying a Nat.succ to our original problem:
let ind_a = Equal/apply (x => (Nat/succ x)) (Problems.t3 n m )Then we invoke our already solved problem, Problems.t2:
let ind_b = Problems.t2 m nWhen we give the Type Check, the terminal returns:
+ INFO Inspection.
• Expected: (Equal Nat (Nat.succ (Plus n m)) (Plus m (Nat.succ n)))
• Context:
• n : Nat
• m : Nat
• ind_a : (Equal Nat (Nat.succ (Plus n m)) (Nat.succ (Plus m n)))
• ind_a = (Equal.apply Nat Nat (Plus n m) (Plus m n) (x => (Nat.succ x)) (Problems.t3 n m))
• ind_b : (Equal Nat (Plus m (Nat.succ n)) (Nat.succ (Plus m n)))
• ind_b = (Problems.t2 m n)
let ind_b = Problems.t2 m n
?
┬
└Here!
Now we can see that the first part of ind_a is the inverse of the first part of our goal and the first part of ind_b is equal to the second part of the goal, we just need to organize and join the necessary parts. To do this, we will use Equal.mirror and Equal.chain.
let ind_c = Equal/chain ind_b Equal/mirror ind_aAnd ind_c returns a value similar to the desired one:
• Expected: Prop.Equal Data.Nat (Data.Nat.succ (Plus n m)) (Plus m (Data.Nat.succ n))
• ind_c : Prop.Equal Data.Nat (Plus m (Data.Nat.succ n)) (Data.Nat.succ (Plus n m))We can see that one is the other mirrored, to make them equal, we will use Equal.mirror again:
let app = Equal/mirror ind_cWhen we call app, the Type Check returns the message All terms checked and thus we prove, through induction and using another proof, the commutation of addition, that the sum of n and m is equal to the sum of m and n.
More exercises
You can use rewrite or chain in this proof, choose whichever you find easiest.
Plus_swap (n: Nat/) (m: Nat/) (p: Nat/) : Equal/ Nat/ (Plus n (Plus m p)) (Plus m (Plus n p))
Plus_swap n m p = ?Now prove the commutativity of multiplication. (You will probably need to define and prove a separate auxiliary theorem to be used in the proof of this. You may find Plus_swap useful.)
Mult_comm (n: Nat/) (m: Nat/) : Equal/ Nat/ (Mult n m) (Mult m n)
Mult_comm n m = ?Take a piece of paper. For each of the following theorems, first think whether (a) it can be proven using just simplification and rewriting, (b) also requires case analysis (destruction), or (c) also requires induction. Write down your prediction.
Then, fill in the proof. (There is no need to submit your piece of paper; this is just to encourage you to reflect before hacking!)
Lte_refl (n: Nat/) : Equal/ Bool/ Bool/true (Lte n n)
Lte_refl n = ?
Zero_nbeq_s (n: Nat/) : Equal/ Bool/ (Eql (Nat/zero) (Nat/succ n)) Bool/false
Zero_nbeq_s n = ?
And_false_r (b: Bool/) : Equal/ Bool/ (Andb b Bool/false) Bool/false
And_false b = ?
S_nbeq_0 (n: Nat/) : Equal/ Bool/ (Eql (Nat.succ n) Nat/zero) Bool/false
Mult_1_l (n: Nat/) : Equal/ Nat/ (Mult (Nat/succ Nat/zero) n) n
Mult_1_l n = ?
All3_spec (b: Bool/) (c: Bool/) : Equal/ Bool/ (Orb (Orb (Andb b c) (Notb b)) (Notb c)) Bool/true
All3_spec b c = ?
Mult_plus_distr_r (n: Nat/) (m: Nat/) (p: Nat/) : Equal/ Nat/ (Mult (Plus n m) p) (Plus (Mult n p) (Mult m p))
Mult_plus_distr_r n m p = ?
Mult_assoc (n: Nat/) (m: Nat/) (p: Nat/) : Equal/ Nat/ (Mult (Mult m p)) (Mult (Mult n m) p)
Mult_assoc n m p = ?Data Structures
Lists : Working with Structured Data
From now on, we will see structured data, especially lists and pairs, which can contain elements of various types. In the type definition, we will already show them with polymorphic types, but don't worry, we will talk about it in the next chapter. For now, let's just ignore the type and follow the explanation. It will make more sense as we progress in our study.
Data Structures
In an inductive type definition, each constructor can receive any number of arguments -- none like Bool, Empty, or one like Nat -- and we have the Pair that receives two arguments (which can even be other two pairs) and returns a type:
record Pair (a) (b) The two received arguments are transformed into the first component, fst, and the second, snd.
record Pair (a) (b) {
fst : a
snd : b
} The way to construct a pair of Nat is as follows:
Pair.new Nat Nat a b : (Pair a b)Here are two simple functions to extract the first and second components of a pair. The definitions also illustrate how to pattern match on two constructor arguments.
Fst (pair: Pair Nat Nat) : Nat
Fst (Pair.new Nat Nat fst snd) = fstExample 1: (Fst Nat (List Nat) (Pair 2n [1n,2n,3n])) -> 2n
Snd (pair: Pair Nat Nat) : Nat
Snd (Pair.new Nat Nat fst snd) = sndExample 2: (Snd Nat (List Nat) (Pair 2n [1n,2n,3n])) -> [1n,2n,3n]
Some proofs
Let's try to prove some simple facts about pairs. If we declare things in a particular (and slightly peculiar) way, we can complete proofs with just reflexivity:
Surjective_pairing (p: Pair Nat Nat) : Equal (Pair Nat Nat) p (Pair.new (Fst p) (Snd p))
Surjective_pairing (Pair.new Nat Nat fst snd) = Equal.reflBut Equal.refl is not enough if the statement is:
Surjective_pairing (Pair.new Nat Nat fst snd) = Equal.reflSince Kind expects
Equal (Pair Nat Nat) p (Pair.new (Fst p) (Snd p))And received
Equal p pWe must "expose" the internal structure of the pair so that the Type Checker can verify whether p is really equal to Pair.new (Fst p) (Snd p).
Snd_fst_is_swap
Snd_fst_is_swap (p: Pair Nat Nat ) : Equal (Pair Nat Nat) (Pair.swap Nat Nat (Pair.swap Nat Nat p) p)
Snd_fst_is_swap (Pair.new Nat Nat fst snd) = ? Fst_swap_is_snd
Fst_swap_is_inverse (p: Pair Nat Nat) (a: Nat) (b: Nat) : Equal (Pair Nat Nat) (Pair.swap Nat Nat (Pair.new a b) (Pair.new b a))
Fst_swap_is_inverse p a b = ?Number Lists
Generalizing the definition of pairs, we can describe the type of number lists as follows: "A list is either the empty list or a set of one element and another list", this type is not composed of a head and a tail.
type List (t) {
nil
cons (head: t) (tail: List t)
}As we are dealing with only one type, it is interesting to rewrite the list type for a defined one, the chosen one was Nat:
type NatList {
nil
cons (head: Nat) (tail: NatList)
}or
type NatList {
List Nat
}We can see that in both notations, there is a head and a tail, with the
head receiving an element of type Nat and the tail receiving a list of type Nat.
For example, a list of three natural numbers 1n, 2n, and 3n would be written as follows:
[1n, 2n, 3n]
However, the Kind reads it differently:
[1n, [2n, 3n]]
where 1n is the head and [2n, 3n] is the tail. Likewise, looking at a
list of 4 elements [1n, 2n, 3n, 4n], we now see it as follows:
[1n, [2n, [3n, 4n]]]
The list has the head 1n and the tail [2n, [3n, 4n]], which, in turn, has the
head 2n and the tail [3n, 4n] which also has its head 3n and its tail 4n.
It may seem scary, but it's a friendly monster:
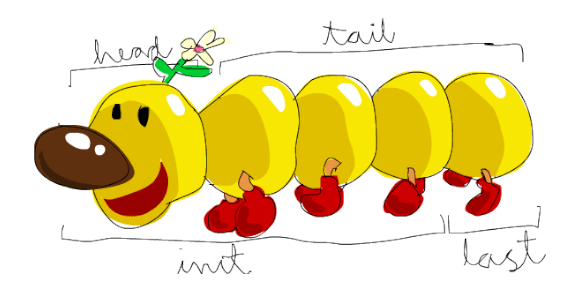
[image font: http://learnyouahaskell.com/starting-out]
Repeat
The function repeat takes a number n and a value, returning a list of size n where all elements are the declared value.
// Example: (Repeat 3 Bool.true) -> [True, True, True]
Repeat (x: Nat) (count: Nat) : List Nat
Repeat x Nat.zero = []
Repeat x (Nat.succ count) = List.cons Nat x (Repeat count x)Length
The function length calculates the size of the list.
// Example: (Length [1,2,3]) -> 3
Length (xs: List Nat) : Nat
Length List.nil = 0n
Length (List.cons head tail) = (Nat.succ (Length tail))Concat
The function concat concatenates (appends) two lists.
Concat (xs: List Nat) (ys: List Nat) : List Nat
Concat (List.nil) ys = ys
Concat (List.cons head tail) ys = List.cons Nat head (Concat tail ys)Head and Tail
The head function returns the first element (the "head") of the list, while tail returns everything except the first element (the "tail"). Of course, an empty list has no first element, so we must handle this case with a Maybe type, receiving a Maybe.none if the list is empty or a Maybe.some if it has a value.
// Example: (Head 0n [1n,2n,3n]) -> 1n
Head (default: Nat) (xs: List Nat) : Nat
Head default (List.nil) = default
Head default (List.cons head tail) = head// Example: (Tail Nat [1,2,3]) -> [2,3]
Tail (xs: List Nat) : List Nat
Tail (List.nil) = []
Tail (List.cons head tail) = tailTest_head1 : Equal Nat (Head 0n [1n,2n,3n]) 1n
Test_head1 = Equal.reflTest_head2 : Equal Nat (Head 0n List.nil) 0n
Test_head2 = Equal.reflTest_head3 : Equal (List Nat) (Tail [1n, 2n, 3n]) [2n, 3n]
Test_head3 = Equal.reflExercises
List_funs
Complete the definitions of Nonzeros, Oddmembers, and Countoddmembers below. Take a look at the tests to understand what these functions should do.
Nonzeros (xs: List Nat) : List Nat
Nonzeros xs = ?Test_nonzeros : Equal (List Nat) (Nonzeros [0n,1n,0n,2n,3n,0n,0n]) [1n,2n,3n]
Test_nonzeros = ?Oddmembers (xs: List Nat) : List Nat
Oddmembers xs = ?Test_oddmembers : Equal (List Nat) (Oddmembers [0n,1n,0n,2n,3n,0n,0n]) [1n,3n]
Test_oddmembers = ?CountOddMembers (xs: List Nat) : Nat
CountOddMembers xs = ?Test_countoddmembers1 : Equal Nat (CountOddMembers [1n,0n,3n,1n,4n,5n]) 4n
Test_countoddmembers1 = ?Alternate
Complete the definition of alternate, which compacts two lists into one, alternating between elements taken from the first list and elements from the second. See the tests below for more specific examples.
Alternate (xs: List Nat) (ys: List Nat) : List Nat
Alternate xs ys = ?Test_alternate1 : Equal (List Nat) (Alternate [1n,2n,3n] [4n,5n,6n]) [1n,4n,2n,5n,3n,6n]
Test_alternate1 = ?Test_alternate2 : Equal (List Nat) (Alternate [1n] [4n,5n,6n]) [1n,4n,5n,6n]
Test_alternate2 = ?Test_alternate3 : Equal (List Nat) (Alternate [1n,2n,3n] [4n]) [1n,4n,2n,3n]
Test_alternate3 = ? Test_alternate4 : Equal (List Nat) (Alternate [] [20n,30n]) [20n,30n]
Test_alternate4 = ?Functions
Complete the following definitions for the count, sum, add, and member functions of natural number lists.
Count (v: Nat) (xs: List Nat) : Nat
Count v xs = ?Test_count1 : Equal Nat (Count 1n [1n,2n,3n,1n,4n,1n]) 3n
Test_count1 = ?Test_count2 : Equal Nat (Count 6n [1n,2n,3n,1n,4n,1n]) 0n
Test_count2 = ?Sum (xs: List Nat) (ys: List Nat) : List Nat
Sum xs ys = ?Test_sum1 : Equal Nat (Count 1n (Sum [1n,2n,3n] [1n,4n,1n])) 3n
Test_sum1 = ?Add (n: Nat) (xs: List Nat) : List Nat
Add n xs = ?Test_add1 : Equal Nat (Count 1n (Add 1n [1n,4n,1n])) 3n
Test_add1 = ?Test_add2 : Equal Nat (Count 5n (Add 1n [1n,4n,1n])) 0n
Test_add2 = ?Member (v: Nat) (xs: List Nat) : Bool
Member v xs = ?Test_member1 : Equal Bool (Member 1n [1n,4n,1n]) Bool.true
Test_member1 = ?Test_member2 : Equal Bool (Member 2n [1n,4n,1n]) Bool.false
Test_member2 = ?More_functions
Here are some more functions of List Nat for you to practice with. When remove_one is applied to a list without the number to be removed, it should return the same unchanged list.
Remove_one (v: Nat) (xs: List Nat) : List Nat
Remove_one v xs = ?Test_remove_one1 : Equal Nat (Count 5n (Remove_one 5n [2n,1n,5n,4n,1n])) 0n
Test_remove_one1 = ?Test_remove_one2 : Equal Nat (Count 5n (Remove_one 5n [2n,1n,4n,1n])) 0n
Test_remove_one2 = ?Test_remove_one3 : Equal Nat (Count 4n (Remove_one 5n [2n,1n,5n,4n,1n,4n])) 2n
Test_remove_one3 = ?Test_remove_one4 : Equal Nat (Count 5n (Remove_one 5n [2n,1n,5n,4n,5n,1n,4n])) 1n
Test_remove_one4 = ?Remove_all (v: Nat) (xs: List Nat) : List Nat
Remove_all v xs = ?Test_remove_all1 : Equal Nat (Count 5n (Remove_all 5n [2n,1n,5n,4n,1n])) 0n
Test_remove_all1 = ?Test_remove_all2 : Equal Nat (Count 5n (Remove_all 5n [2n,1n,4n,1n])) 0n
Test_remove_all2 = ?Test_remove_all3 : Equal Nat (Count 4n (Remove_all 5n [2n,1n,5n,4n,1n,4n])) 2n
Test_remove_all3 = ?Test_remove_all4 : Equal Nat (Count 5n (Remove_all 5n [2n,1n,5n,4n,5n,1n,4n,5n,1n,4n])) 0n
Test_remove_all4 = ?Subset (xs: List Nat) (ys: List Nat) : Bool
Subset xs ys = ?Test_subset1 : Equal Bool (Subset [1n,2n] [2n,1n,4n,1n]) Bool.true
Test_subset1 = ?Test_subset2 : Equal Bool (Subset [1n,2n,2n] [2n,1n,4n,1n]) Bool.false
Test_subset2 = ?Theorem
Write down an interesting theorem involving the count and add functions and prove it. Note that, as this problem is somewhat open-ended, you may come up with a theorem that is true but whose proof requires techniques you have not yet learned. Feel free to ask for help if you get stuck!
Theorem : ?Reasoning about Lists
Just like numbers, simple facts about list processing functions can sometimes be entirely proven by simplification. For example, the simplification performed by Equal.refl is sufficient for this theorem...
`List.nil`_app (xs: List Nat) : Equal (Concat (List.nil Nat) xs) xs
`List.nil`_app xs = Equal.refl...this is because the Type "sees" the List.nil and automatically reduces equality just as it does with natural numbers and Nat.zero.
Furthermore, as with numbers, it is sometimes useful to perform a case analysis on the possible forms (empty or non-empty) of an unknown list.
Tl_length_pred (xs: List Nat) : Equal Nat (Pred (Length xs)) (Length (Tail xs))
Tl_length_pred List.nil = Equal.refl
Tl_length_pred (List.cons head tail) = Equal.reflIf the user does not open the cases and uses Equal.refl directly, the Type returns a type error:
- ERROR Type mismatch
• Got : Equal Nat (Nat.pred (Length xs)) (Nat.pred (Length xs))
• Expected : Equal Nat (Nat.pred (Length xs)) (Length (Tail xs))
• Context:
• xs : (List Nat)
Tl_length_pred xs = Equal.refl
┬─────────
└Here!
Similarly, some theorems require induction for their proofs.
- Micro-Sermon. Simply reading example proof scripts won't get you very far! It's important to work through the details of each one, using the Type and thinking about what each step achieves. Otherwise, it's more or less guaranteed that the exercises won't make sense when you get to them. ( ಠ ʖ̯ ಠ)
Induction on Lists
Proofs by induction on data types like List are a bit less familiar than standard natural number induction, but the idea is equally simple. Each data declaration defines a set of data values that can be constructed using the declared constructors: a boolean can be True or False; a number can be Zero or Succ applied to another number; a list of naturals can be List.nil or List.cons applied to a number and a list.
Moreover, the applications of the declared constructors to each other are the only possible forms that elements of an inductively defined set can have, and this fact directly gives rise to a way of reasoning about inductively defined sets: a number is Zero or else it is Succ applied to a smaller number; a list is List.nil or else it is a List.cons applied to some number and a smaller list, etc. So, if we have in mind some proposition p that mentions a listl and we want to argue that p holds for all lists, we can reason as follows:
- First, show that
pis true forlwhenlisList.nil. - Then show that
pis true forlwhenlisList.cons n lfor some numbernand some smaller listl, assuming thatpis true forl.
Since larger lists can only be constructed from smaller lists, eventually reaching List.nil, these two arguments together establish the truth of p for all lists l. Here's a concrete example:
Concat_assoc (xs: List Nat) (ys: List Nat) (zs: List Nat) : Equal (Concat (Concat xs ys) zs) (Concat xs (Concat ys zs))
Concat_assoc List.nil ys zs = Equal.refl
Concat_assoc (List.cons Nat xs.head xs.tail) ys zs =
let ind = Concat_assoc xs.tail ys zs
let app = Equal.apply (x => (List.cons xs.head x)) ind
appWe are given three lists xs, ys, and zs and we check if concatenating xs and ys with zs is equal to concatenating xs with the concatenation of ys and zs.
For this, we check for the case where xs is an empty list, then we receive a reflection that the concatenation is between ys and zs, and it suffices to give an Equal.refl.
Next, we "open up" xs to obtain xs.tail for our induction, and we receive as the objective:
• Expected: Equal (List Nat) (List.cons Nat xs.head (Concat (Concat xs.tail ys) zs)) (List.cons Nat xs.head (Concat xs.tail (Concat ys zs)))
and our ind variable is:
• ind: Equal (List Nat) (Concat (Concat xs.tail ys) zs) (Concat xs.tail (Concat ys zs))
it is sufficient to apply a List.cons xs.head on both sides of the equality to obtain the final objective, which is what we do in app:
• app : Equal (List Nat) (List.cons Nat xs.head (Concat (Concat xs.tail ys) zs)) (List.cons Nat xs.head (Concat xs.tail (Concat ys zs)))
NOTE
e Type Check returns types t2, t3, and others generated in the same style, which we can ignore and even delete when comparing the return of variables, as we see in the following case
• Expected: Equal (List Nat) (List.cons Nat xs.head (Concat (Concat xs.tail ys) zs)) (List.cons Nat xs.head (Concat xs.tail (Concat ys zs)))
• app : Equal (List Nat) (List.cons Nat xs.head (Concat (Concat xs.tail ys) zs)) (List.cons Nat xs.head (Concat xs.tail (Concat ys zs)))
This way it's easier to see that app and Expected are identical, so there's no need to be alarmed when seeing these generated types.
Reversing a list
For a slightly more complicated example of inductive proof about lists, suppose we use Concat to define a list reversal function Rev:
Rev (xs: List Nat) : List Nat
Rev List.nil = List.nil Nat
Rev (List.cons head tail) = Concat (Rev tail) [head]
Test_rev1 : Equal (List Nat) (Rev [1n,2n,3n]) [3n,2n,1n]
Test_rev1 = Equal.refl
Test_rev2 : Equal (Rev List.nil) List.nil
Test_rev2 = Equal.reflProperties of Rev
Now let's prove some theorems about the Rev we just defined. For something a bit more challenging than what we've seen, let's prove that reversing a list doesn't change its length. Our first attempt gets stuck at the successor case...
Rev_length_firsttry (xs: List Nat) : Equal Nat (Length (Rev xs)) (Length xs)
Rev_length_firsttry List.nil = Equal.refl
Rev_length_firsttry (List.cons xs.head xs.tail) =
let ind = Rev_length_firsttry xs.tail
?The Type Check returns the following goal and context:
+ INFO Inspection.
• Expected: Equal Nat (Length (Concat (Rev tail) (List.cons Nat head (List.nil Nat)))) (Nat.succ (Length tail))
• Context:
• head : Nat
• tail : (List Nat)
• ind : Equal Nat (Length (Rev tail)) (Length tail)
• ind = (Rev_length_firsttry tail)
let ind = Rev_length_firsttry tail
?
┬
└Here!
Now we have to prove that the length of the concatenation of the reverse of the tail of the list and its head is equal to the successor of the length of the tail, so we'll need to use some other proofs, one of which is that the length of the concatenation of two lists is the same as the sum of the lengths of each of them:
Concat_length (xs: List Nat) (ys: List Nat) : Equal Nat (Length (Concat xs ys)) (Plus (Length xs) (Length ys))
Concat_length List.nil ys = Equal.refl
Concat_length (List.cons xs.head xs.tail) ys =
let ind = Concat_length xs.tail ys
let app = Equal.apply (x => (Nat.succ x)) ind
appIn addition to this proof, we'll use others already proven in previous chapters:
Plus_n_z (n: Nat) : Equal Nat n (Plus n Nat.zero)
Plus_n_sn (n: Nat) (m: Nat) : Equal Nat (Nat.succ (Plus n m)) (Plus n (Nat.succ m))
Plus_comm (n: Nat) (m: Nat) : Equal Nat (Plus n m) (Plus m n)And now we can prove our theorem:
Rev_length (xs: List Nat) : Equal Nat (Length (Rev xs)) (Length xs)
Rev_length List.nil = Equal.refl
Rev_length (List.cons Nat head tail) =
let ind = Rev_length tail
?+ INFO Inspection.
• Expected: Equal Nat (Length (Concat (Rev tail) (List.cons Nat head (List.nil Nat)))) (Nat.succ (Length tail))
• Context:
• head : Nat
• tail : (List Nat)
• ind : Equal Nat (Length (Rev tail)) (Length tail)
• ind = (Rev_length tail)
let ind = Rev_length tail
?
┬
└Here!
We create a variable with our auxiliary Concat_length:
Rev_length (xs: List Nat) : Equal Nat (Length (Rev xs)) (Length xs)
Rev_length List.nil = Equal.refl
Rev_length (List.cons Nat head tail) =
let ind = Rev_length tail
let aux1 = Concat_length (Rev xs.tail) [xs.head]
?We receive a new context for our auxiliaries...
• aux1: Equal Nat (Length (Concat (Rev tail) (List.cons Nat head (List.nil Nat)))) (Plus (Length (Rev tail)) 1n)
... the aux1 is equal to the left side of our Expected, so half the work is already done, we just need the other side of the equality and for that we create a new variable, aux2:
let aux2 = Plus_comm (Length (Rev xs.tail)) (1n)Now our context is even better:
• aux2: Equal Nat (Plus (Length (Rev tail)) 1n) (Nat.succ (Length (Rev tail))) As we make progress in our formal proofs, we can see that the left side of aux2 is equal to the right side of aux1, and we can chain them together using Equal.chain:
let chn = Equal.chain aux1 aux2When we Type Check, we see our new context:
• chn : Equal Nat (Length (Concat (Rev tail) (List.cons Nat head (List.nil Nat)))) (Nat.succ (Length (Rev tail)))
Our chn variable is practically identical to our Expected, differing only in the final part, since Expected expects a Nat.succ (Length xs.tail) and chn gives us Nat.succ (Length (Rev xs.tail)), but we have the ind variable that returns us this equality. Let's remember:
• ind: Equal Nat (Length (Rev tail)) (Length tail)
Incredible, isn't it? It returns exactly what we need, that the size of the reverse of the tail is equal to the size of the tail, so we just need to rewrite the ind variable in our chn:
let rrt = Equal.rewrite ind (x => Equal Nat (Length (Concat (Rev tail) (List.cons head (List.nil)))) (Nat.succ x )) chnLet's see our new context, only hiding the types for easier reading:
+ INFO Inspection.
• Expected: Equal Nat (Length (Concat (Rev tail) (List.cons _ head (List.nil _)))) (Nat.succ (Length tail))
• Context:
• head : Nat
• tail : (List Nat)
• ind : Equal Nat (Length (Rev tail)) (Length tail)
• ind = (Rev_length tail)
• aux1 : Equal Nat (Length (Concat (Rev tail) (List.cons Nat head (List.nil Nat)))) (Plus (Length (Rev tail)) 1n)
• aux1 = (Concat_length (Rev tail) (List.cons Nat head (List.nil Nat)))
• aux2 : Equal Nat (Plus (Length (Rev tail)) 1n) (Nat.succ (Length (Rev tail)))
• aux2 = (Plus_comm (Length (Rev tail)) 1n)
• chn : Equal Nat (Length (Concat (Rev tail) (List.cons Nat head (List.nil Nat)))) (Nat.succ (Length (Rev tail)))
• chn = Equal.chain Nat (Length (Concat (Rev tail) (List.cons Nat head (List.nil Nat)))) (Plus (Length (Rev tail)) 1n) (Nat.succ (Length (Rev tail))) aux1 aux2
• rrt : Equal Nat (Length (Concat (Rev tail) (List.cons Nat head (List.nil Nat)))) (Nat.succ (Length tail))
• rrt = Equal.rewrite Nat (Length (Rev tail)) (Length tail) ind (x => Equal Nat (Length (Concat (Rev tail) (List.cons Nat head (List.nil Nat)))) (Nat.succ x))) chn
Now it's much easier to see that our rrt is exactly our Expected, so our proof is as follows:
Rev_length (xs: List Nat) : Equal Nat (Length (Rev xs)) (Length xs)
Rev_length List.nil = Equal.refl
Rev_length (List.cons Nat head tail) =
let ind = Rev_length tail
let aux1 = Concat_length (Rev tail) [head]
let aux2 = Plus_comm (Length (Rev tail)) (1n)
let chn = Equal.chain aux1 aux2
let rrt = Equal.rewrite ind (x => Equal Nat (Length (Concat (Rev tail) [head])) (Nat.succ x)) chn
rrtList Exercises, Part 1
List_exercises
Let's practice a little more with lists:
Concat_nil_r (xs: List Nat) : Equal (Concat xs List.nil) xs
Concat_nil_r xs = ?
Concat_assoc (xs: List Nat) (ys: List Nat) (zs: List Nat) : Equal (Concat (Concat xs ys) zs) (Concat xs (Concat ys zs))
Concat_assoc xs ys zs = ?
Rev_app_distr (xs: List Nat) (ys: List Nat) : Equal (Rev (Concat xs ys)) (Concat (Rev ys) (Rev xs))
Rev_app_distr xs ys = ?
Rev_involutive (xs: List Nat) : Equal (Rev (Rev xs)) xs
Rev_involutive xs = ?There is a short solution to the next one. If you find it too difficult or it starts to get too long, step back and try to find a simpler way.
Concat_assoc4 (l1: List Nat) (l2: List Nat) (l3: List Nat) (l4: List Nat) : Equal (List Nat) (Concat l1 (Concat l2 (Concat l3 l4))) (Concat (Concat (Concat l1 l2) l3) l4)
Concat_assoc4 l1 l2 l3 l4 = ? An exercise on your implementation of Nonzeros:
Nonzeros_app (xs: List Nat) (ys: List Nat) : Equal (List Nat) (Nonzeros (Concat xs ys)) (Concat (Nonzeros xs) (Nonzeros ys))
Nonzeros_app xs ys = ?Beq_NatList
Fill in the definition of beq_NatList, which compares lists of numbers for equality. Prove that beq_NatList xs ys produces Bool.true for each list.
Beq_NatList (xs: List Nat) (ys: List Nat) : Bool
Beq_NatList xs ys = ?
Test_beq_natlist1 : Equal Bool (Beq_list List.nil List.nil) Bool.true
Test_beq_natlist1 = ?
Test_beq_natlist2 : Equal Bool (Beq_list [1n,2n,3n] [1n,2n,3n]) Bool.true
Test_beq_natlist2 = ?
Test_beq_natlist3 : Equal Bool (Beq_list [1n,2n,3n] [1n,2n,4n]) Bool.false
Test_beq_natlist3 = ?
Beq_natlist_refl (xs: List Nat) : Equal Bool Bool.true (Beq_list xs xs)
Beq_natlist_refl xs = ?List Exercises, Part 2
Proofs
Prove the following theorem, it will help you in the next proof:
Ble_n_succ_n (n: Nat) : Equal Bool (Lte n (Nat.succ n)) Bool.true
Ble_n_succ_n n = ? Prove the following theorem, it will help you in the next proof:
Count_member_nonzero (xs: List Nat) : Equal Bool (Lte 1n (Count 1n (List.cons 1n xs))) Bool.true
Count_member_nonzero xs = ?Rev_injective
Prove that the Rev function is injective - that is,
Rev_injective (xs: List Nat) (ys: List Nat) (e: Equal (List Nat) (Rev xs) (Rev ys)) :tail Equal (List Nat) xs ys
Rev_injective xs ys e = ? Optional: Count_sum
Write an interesting theorem about Lists involving the functions count and sum, and prove it. (You may find that the difficulty of the test depends on how you set the count!)
Count_sum : ?
Maybe
Suppose we want to write a function that returns the nth number of a list. We then define a number that is applied to a list of naturals and returns the number that occupies that position. Therefore, we need to define a number to be returned if the number is greater than the size of the list.
Nth_bad (n: Nat) (xs: List Nat) : Nat
Nth_bad n List.nil = 42n // arbitrary value
Nth_bad Nat.zero (List.cons head tail) = head
Nth_bad (Nat.succ n) (List.cons head tail) = Nth_bad n tailThis solution is not so good: if nth_bad returns 0, we cannot tell if that value actually appears in the input without further processing. A better alternative is to change the return type of nth_bad to include an error value as a possible result.
We call this type Maybe, because it may or may not have something; if it has, it is a Maybe.some of that something, if it does not have, it is a Maybe.none.
type Maybe (t) {
none
some (value: t)
}We can then change the above definition of nth_bad to return None when the list is too short and Some when the list has enough members and appears at the position n. We call this new function nth_error to indicate that it may result in an error.
This proof also serves to introduce us to another feature of Kind, conditional expressions, the if and else.
Nth_error (n: Nat) (xs: List Nat) : Maybe Nat
Nth_error n List.nil = Maybe.none
Nth_error n (List.cons head tail) =
let ind = Nth_error (Pred n) tail
Bool.if (Eql n 0n) (Maybe.some Nat head) (ind)
Test_nth_error1 : Equal (Nth_error 0n [4n,5n,6n,7n]) (Maybe.some 4n)
Test_nth_error1 = Equal.refl
Test_nth_error2 : Equal (Nth_error 3n [4n,5n,6n,7n]) (Maybe.some 7n)
Test_nth_error2 = Equal.refl
Test_nth_error3 : Equal (Nth_error 9n [4n,5n,6n,7n]) Maybe.none
Test_nth_error3 = Equal.reflExtract (d: Nat) (o: Maybe Nat) : Nat
Extract d (Maybe.some k) = k
Extract d (Maybe.none) = dHead_error
Using the same idea, correct the Head function from before so that we don't have to pass a default element for the case List.nil.
Head_error (xs: List Nat) : Maybe Nat
Head_error xs = ?
Test_head_error1 : Equal (Head_error List.nil) Maybe.none
Test_head_error1 = ?
Test_head_error2 : Equal (Head_error [1n]) (Maybe.some Nat 1n)
Test_head_error2 = ?
Test_head_error3 : Equal (Head_error [5n,6n]) (Maybe.some Nat 5n)
Test_head_error3 = ?Optional: Extract_head
This exercise relates your new Head_error to the old Head.
Extract_head (l: List Nat) (default: Nat) : Equal Nat (Head default l) (Extract default (Head_error l))
Extract_head l default = ?Polymorphism
In this chapter, we continue our development of basic programming concepts. Our new essential principles are polymorphism (abstraction functions over the data types they manipulate) and higher-order functions (treating functions as data). We begin with polymorphism.
Polymorphic Lists
In the last two chapters, we worked with polymorphic lists, you may just not have realized it. Obviously, interesting programs also need to be able to manipulate lists with elements of other types - lists of strings, lists of booleans, lists of lists, etc. We could just define a new inductive data type for each of them, for example...
type BoolList {
nil
cons (head: Bool) (tail: List Bool)
}...but that would quickly become tedious, in part because we have to compensate for different constructor names for each data type, but mainly because we also need to define new versions of all our list manipulation functions (length, rev, etc.) for each new data type definition.
To avoid all this repetition, Kind supports definitions of polymorphic inductive types. For example, here is a polymorphic list data type that we already saw in the previous chapter:
type List (t) {
nil
cons (head: t) (tail: List t)
}This type already exists in Kind and we can see that it is identical to BoolList, but with a type a, which receives any other type, be it Nat, Bool, Maybe, etc. We don't need to create a list type for each of the data types, we can use this one that adopts all existing forms.
What kind of thing is the List itself? A good way to think about it is that List is a Types function for inductive definitions; or, in other words, List is a Types function for Types. For any specific type x, the type List x is an inductively defined set of lists whose elements are of type x.
With this definition, when we use the constructors List.nil and List.cons to build lists, we need to tell Kind the type of elements in the lists we are building - that is, that List.nil and List.cons are now polymorphic constructors. Note the types of constructors:
record Pair (a) (b) {
fst : a
snd : b
}Our Pair type receives two other types, a and b, and returns a pair of the two types. It was not necessary to define whether the pair was of natural numbers, booleans, lists, bits or other pairs, we left the function capable of handling all possible pairs and this is thanks to polymorphism.
Now we can go back and make polymorphic versions of all the processing lists functions we wrote before. Here's the repeat function again, for example:
Repeat <a: Type> (x: a) (count: Nat) : List a
Repeat a x Nat.zero = List.nil
Repeat a x (Nat.succ count) = List.cons x (Repeat x count)Just like with List.nil and List.cons, we can use repeat by first applying it to a type and then to its list argument:
Test_repeat1 : Equal (Repeat 4n 2n) (List.cons 4n (List.cons 4n List.nil))
Test_repeat1 = Equal.reflTo use repeat to build other types of lists, we simply instantiate it with an appropriate type parameter:
Test_repeat2 : Equal (Repeat Bool.false 1n) (List.cons Bool.false List.nil)
Test_repeat2 = Equal.reflType Annotation Inference
Let's write the definition of repeat again, but this time omitting the type. However, please note that this is not a good practice to use the hole, it will only serve to understand the power of Kind and how it can help the user find what they want.
Repeat (x: _) (count: Nat) : List _
Repeat x Nat.zero = ?When running the Type Check, the terminal returns:
+ INFO Inspection.
• Expected: (List _)
• Context:
• x : _
Repeat x Nat.zero = ?
┬
└Here!
For the case where the count is zero, which is our stopping point, we need to return a list of undefined type.
As we did when our type was defined, we are creating a list that does not repeat the term at all, we return a List.nil, then we check for the case of a list that will repeat the value count times, for this we will use recursion through Nat.succ pred, that is, our count is equal to the successor of its predecessor.
Repeat x (Nat.succ count) = ?And the Type Check returns:
+ INFO Inspection.
• Expected: (List _)
• Context:
• x : _
• count : Nat
Repeat x (Nat.succ count) = ?
┬
└Here!
Now we just need to construct the list with the value and call the function for the predecessor of count, thus building the list until it reaches zero.
Repeat (x: _) (count: Nat) : List _
Repeat x Nat.zero = List.nil
Repeat x (Nat.succ count) = List.cons x (Repeat x count)We can see that, even though we didn't define the type of x, the Kind is powerful enough to discover the type that our x is when we use the _ hole. Although it is possible and may even facilitate building an entire application using this notation, it is not a good practice since, depending on the case, a different type than the desired one may be inferred. It is interesting to always define the type of our element, even if it is a polymorphic type.
In the first case, when we define the type a, we already encompass all possible types, so it is not necessary to use the hole and that is the magic of polymorphism, it allows us to use the same function for different types.
To use a polymorphic function, we need to pass one or more types in addition to the other arguments. For example, in the case of repeat, we pass the type <a: Type> and that each element of our list is of that type. We did the same with the Pair type, which received two types a and b as arguments.
Now it is much easier to understand the examples we used in the previous chapter, when we presented functions like length and append:
Length <a> (xs: List a) : Nat
Length (List.nil t) = Nat.zero
Length (List.cons t head tail) = (Nat.succ (Length tail))
Concat <a: Type> (xs: List a) (ys: List a) : List a
Concat (List.nil) ys = ys
Concat (List.cons head tail) ys = List.cons head (Concat tail ys)
Note that there are two notations, one where we only use <a> and another where we use <a: Type>, we can use either one, the Kind is capable of understanding both forms, it will be up to the developer to choose which one to use and the complexity of what will be developed, since in very complex code, it may be interesting to make explicit to other programmers what each thing is.
Now it's time to implement our functions with implicit typing, using hole and sugar syntax:
Concat_implicit (xs: List _) (ys: List _) : List _
Concat_implicit [] ys = ys
Concat_implicit (List.cons head tail) ys = List.cons head (Concat_implicit tail ys)Here we learned one more thing, the sugar syntax for an empty list is just [], but this is wrong, since the sugar syntax for kind doesn't work on the left side of the function scope, only on the right side. Using the wrong sugar syntax results in an error shown by Kind:
- ERROR Unexpected token '['.
Concat_implicit [] ys = ys
┬
└Here!
Therefore, it is always important to know exactly what is being done, especially when using sugar syntax. It is meant to make our lives easier but can cause problems when used incorrectly. This also applies to hole and polymorphic types help us write a safer program that can be used for countless cases.
We can also rewrite the reverse function:
Rev <a> (xs: List a) : List a
Rev List.nil = [] // sugar syntax de List.nil
Rev (List.cons head tail) = Concat (Rev tail) [head] // sugar syntax de (List.cons head List.nil)
Length <a> (xs: List a) : Nat
Length List.nil = 0n // sugar syntax de Nat.zero
Length (List.cons head tail) = Nat.succ (Length tail)After that, we just need to prove that our functions are correct:
Test_rev1 : Equal (Rev [1,2,3]) [3,2,1]
Test_rev1 = Equal.refl
Test_rev2 : Equal (Rev [Bool.true]) [Bool.true]
Test_rev2 = Equal.refl
Test_length1 : Equal (Length [1,2,3]) 3n
Test_length1 = Equal.reflPolymorphic Exercises
Here are some simple exercises, similar to the ones in the Lists section, to practice polymorphism. Complete the proofs below.
Concat_nil_r <a> (xs: List a) : Equal (Concat xs List.nil) xs
Concat_nil_r xs = ?
Concat_assoc <a> (xs: List a) (ys: List a) (zs: List a) : Equal (Concat xs (Concat ys zs)) (Concat (Concat xs ys) zs)
Concat_assoc xs ys zs = ?
Concat_length <a> (xs: List a) (ys: List a) : Equal (Length (Concat xs ys)) (Plus (Length xs) (Length ys))
Concat_length xs ys = ?More Polymorphic Exercises
Here are some slightly more interesting exercises...
Rev_app_distr <a> (xs: List a) (ys: List a) : Equal (Rev (Concat xs ys)) (Concat (Rev ys) (Rev xs))
Rev_app_distr xs ys = ?
Rev_involutive <a> (xs: List a) : Equal (Rev (Rev xs)) xs
Rev_involutive xs = ?Polymorphic Pairs
Following the same pattern, the type definition for pairs of numbers that we gave in the last chapter can be generalized for polymorphic pairs:
record Pair (a) (b) {
fst : a
snd : b
} This is exactly the first definition of pairs that we saw in the previous chapter, and now we can understand perfectly what the a and b types are in the Pair type definition.
We can rewrite the Pairs functions, but now for polymorphic types:
Fst <a> <b> (pair: Pair a b) : a
Fst (Pair.new fst snd) = fst
Snd <a> <b> (pair: Pair a b) : b
Snd (Pair.new fst snd) = sndThe following function takes two lists and combines them into a list of pairs. In functional languages, this is commonly called Zip.
Zip <a> <b> (xs: List a) (ys: List b) : (List (Pair a b))
Zip [] ys = []
Zip xs [] = []
Zip (List.cons xs.h xs.t) (List.cons ys.h ys.t) = List.cons (Pair.new xs.h xs.t) (Zip xs.t ys.t)Check
Without running the program, try to answer the following question:
- What will the combination of
[1, 2]and[Bool.true, Bool.false, Bool.false, Bool.true]return?
Now run the code and see if you got it right.
Split
The Split function is the inverse of Zip. It takes a list of pairs and returns a pair of lists. In many functional languages, it is called Unzip.
Fill in the definition of the splitting function below. Make sure it passes the unit test provided.
Split <a> <b> (xs: List (Pair a b)) : Pair (List a) (List b)
Split xs = ?
Test_split : Equal (Split [(Pair.new 1 Bool.false), (Pair.new 2 Bool.false)]) (Pair.new ([1, 2]) ([Bool.false, Bool.false]))
Test_split = ?Polymorphism with Maybe
In the previous chapter, we also saw the Maybe type, but only for natural types. However, as we have seen in this chapter, our data structures can be polymorphic, which means that the Maybe type is also polymorphic, and that is what we will see now.
type Maybe (t) {
none
some (value: t)
}This way, we can write the function of the nth error to be used with all types of lists:
Nth_error <a> (n: Nat) (xs: List a) : Maybe a
Nth_error a n List.nil = Maybe.none
Nth_error a n (List.cons head tail) =
let ind = Nth_error (Pred n) tail
Bool.if (Eql n 0n) (Maybe.some head) (ind)
Test_nth_error1 : Equal (Nth_error 0n [4n,5n,5n,7n]) (Maybe.some 4n)
Test_nth_error1 = Equal.refl
Test_nth_error2 : Equal (Nth_error 2n [Bool.true]) Maybe.none
Test_nth_error2 = Equal.refl
Test_nth_error3 : Equal (Nth_error 1n [[1n],[2n]]) (Maybe.some [2n])
Test_nth_error3 = Equal.refl
Hd_error
Complete the definition of a polymorphic version of the Hd_error function from the last chapter. Make sure it passes the unit tests below.
Hd_error <a> (xs: List a) : Maybe a
Hd_error xs = ?
Test_hd_error1 : Equal (Hd_error [1, 2]) (Maybe.some 1)
Test_hd_error1 = ?
Test_hd_error2 : Equal (Hd_error [[1], [2]]) (Maybe.some [1])
Test_hd_error2 = ?Functions as data
Functions as data Like many other modern programming languages -- including all functional languages (ML, Haskell, Scheme, Scala, Clojure, etc.) -- Kind treats functions as first-class citizens, allowing them to be passed as arguments to other functions, returned as results, stored in data structures, etc.
Higher-Order Functions
Functions that manipulate other functions are often called higher-order functions (or "higher-order" for short). Here is a simple example:
Doit3times <x> (f: x -> x) (n: x) : x
Doit3times f x = (f (f (f x)))
Test_doit3times1 : Equal (Doit3times (x => MinusTwo x) 9n) 3n
Test_doit3times1 = Equal.refl
Test_doit3times2 : Equal (Doit3times (x => Notb x) Bool.true) (Bool.false)
Test_doit3times2 = Equal.reflFilter
Here is a more useful higher-order function, taking a list of xs and a predicate on x (a function from x to Bool) and "filtering" the list, returning a new list containing only those elements for which the predicate returns Bool.true.
Filter <x> (test: x -> Bool) (xs: List x) : List x
Filter test List.nil = []
Filter test (List.cons head tail) =
Bool.if (test head) (List.cons head (Filter test tail)) (Filter test tail)For example, if we apply the "is even" filter to a list of numbers, it will return another list with only the even numbers.
Test_filter1 : Equal (Filter (x => Evenb x) [1,2,3,4,5]) [2,4]
Test_filter1 = Equal.refl
Length_is_one <x> (xs: List x) : Bool
Length_is_one xs = Eql (Length xs) 1n
Test_filter2 : Equal (Filter (x => Length_is_one x) ([[1],[1,2],[3],[1,2,3],[21]])) ([[1],[3],[21]])
Test_filter2 = Equal.reflWe can use filter to provide a concise version of the Countoddmembers function from the Lists chapter.
CountOddMembers (xs: List Nat) : Nat
CountOddMembers xs = Length (Filter (x => Oddb x) xs)
Test_CountOddMembers1 : Equal (CountOddMembers [1n,0n,3n,1n,4n,5n]) 4n
Test_CountOddMembers1 = Equal.refl
Test_CountOddMembers2 : Equal (CountOddMembers [0n 2n,4n]) 0n
Test_CountOddMembers2 = Equal.refl
Test_CountOddMembers3 : Equal (CountOddMembers []) 0n
Test_CountOddMembers3 = Equal.reflAnonymous Functions
It is arguably a bit sad, in the example above, to be forced to define the function Length_is_one and give it a name just to be able to pass it as an argument to filter, since we will probably never use it again.
Furthermore, this is not an isolated example: when using higher-order functions, we often want to pass "unique" functions as arguments that we will never use again; having to name each of these functions would be tedious.
Fortunately, there is a better way. We can build a function "on the fly" without declaring it at the top level or giving it a name.
Test_anon_fun : Equal (Doit3times (x => (Mult x x)) 2n) 256n
Test_anon_fun = Equal.reflThe expression x => (Mult x x) can be read as "the function takes a number n and returns n * n".
Here is the example of Filter rewritten to use an anonymous function:
Test_filter2 : Equal (Filter (x => (Length_is_one x)) [[1],[1,2],[2],[1,2,3],[21]]) [[1],[2],[21]]
Test_filter2 = Equal.refl
Filter_even_gt7
Use Filter with anonymous functions (instead of function definitions) to write a function Filter_even_gt7 that takes a list of natural numbers as input and returns a list only of those that are even and greater than 7.
Filter_even_gt7 (xs: List Nat) : List Nat
Filter_even_gt7 xs = ?
Test_filter_even_gt7a: Equal (Filter_even_gt7 [1n,2n,3n,4n,5n,7n,8n,9n,10n,11n,12n]) [8n,10n,12n]
Test_filter_even_gt7a = ?
Test_filter_even_gt7b : Equal (Filter_even_gt7 [5n, 2n, 6n, 19n, 129n]) []
Test_filter_even_gt7b = ?A small observation, the attentive reader may have noticed that we used a new notation, the n after the numbers. This is a sugar syntax that Kind has. We can write natural numbers by simply adding an n to the number. However, this is a syntax that can end up weighing down Kind. Imagine that the user only wants to add the number 1 to 1000000, it's a simple calculation that Kind can easily handle, but it becomes a bit heavier when using the sugar syntax for natural numbers. The sum will be Plus 1n 1000000n, but Kind will need to check each Nat.succ up to one million and one, in other words, one million and one "Nat.succ" will be computed unnecessarily. This syntax is very useful, but we should use it with care. Ideally, for large numbers, U60.to_nat should be used, which is much lighter for Kind.
Partition
Use Filter to write a Partition function in Kind.
Partition <x> (test: x -> Bool) (xs: List x) : Pair (List x) (List x)
Partition test xs = ?Given a set x, a test function of type x -> Bool, and a List x, the Partition function should return a pair of lists. The first member of the pair is the sublist of the original list containing the elements that satisfy the test, and the second is the sublist containing those that fail the test. The order of the elements in the two sublists should be the same as the original list.
Test_partition1 : Equal (Partition (x => Oddb x) [1n,2n,3n,4n,5n]) (Pair.new [1n,3n,5n] [2n,4n])
Test_partition1 = ?
Test_partition2 : Equal (Partition (x => Bool.false) [5n, 9n, 0n]) (Pair.new [] [5n, 9n, 0n])
Map
Another very useful higher-order function is Map.
Map <x> <y> (f: x -> y) (xs: List x) : List y
Map f List.nil = List.nil
Map f (List.cons head tail) = List.cons (f head) (Map f tail)It takes a function f and a list xs = [n1, n2, n3, ...] and returns the list [f n1, f n2, f n3, ...], where f is applied to each element of xs. For example:
Test_map1 : Equal (Map (x => Plus 3n x) [2n, 0n, 2n]) [5n, 3n, 5n]
Test_map1 = Equal.reflThe types of the elements in the input and output list do not need to be the same, as Map accepts two type arguments, x and y; thus a function of numbers to booleans can be applied to produce a list of booleans:
Test_map2 : Equal (Map (x => Nat.is_odd x) [2n, 1n, 2n, 5n]) [Bool.false, Bool.true, Bool.false, Bool.true]
Test_map2 = Equal.reflIt can even be applied to a list of numbers and a function that returns a list of boolean lists:
Test_map3 = Equal (Map (x => [(Nat.is_even x), (Nat.is_odd x)]) [2n, 1n, 2n, 5n]) [[Bool.true, Bool.false], [Bool.false, Bool.true], [Bool.true, Bool.false], [Bool.false, Bool.true]]
Test_map3 = Equal.reflMap_rev
Let's make things a little more difficult. Show the commutativity of Rev and Map; you may need an auxiliary function:
Map_rev <x> <y> (f: x -> y) (xs: List x) : Equal (Map f (Rev xs)) (Rev (Map f xs))
Map_rev f xs = ?Flat_equal
The Map function maps a List x to a List y using a function of type x -> y. We can define a similar function, Flat_map, that maps a List x to a List y using a function f of type x -> List y. Its definition should work by "flattening" the results of f, like so:
Flat_equal : Equal (Flat_map ( x => ([x , (Plus x 1n), (Plus x 2n)])) [1n, 5n, 10n]) [1n, 2n, 3n, 5n, 6n, 7n, 10n, 11n, 12n]
Flat_equal = Equal.refl
Flat_map <x> <y> (f: x -> List y) (xs: List x) : List y
Flat_map f xs = ?
Test_flat_map1 : Equal (Flat_map (x => [x, x, x]) [1n, 5n, 4n]) [1n, 1n, 1n, 5n, 5n, 5n, 4n, 4n, 4n]
Test_flat_map1 = ?Lists are not the only inductive type for which we can write a Map function. Here's the definition of map for the Maybe type:
Maybe_map <x> <y> (f: x -> y) (a: Maybe x) : Maybe y
Maybe_map f Maybe.none = Maybe.none
Maybe_map f (Maybe.some x) = Maybe.some (f x)Fold
An even more powerful higher-order function is called Fold. This function is the inspiration for the "reduce" operation that is at the heart of Google's map/reduce distributed programming framework.
Fold <x> <y> (f: x -> y -> y) (xs: List x) (a: y) : y
Fold f List.nil a = a
Fold f (List.cons head tail) a = f head (Fold f tail a)
Test_fold1 : Equal (Fold (x => y => (Bool.and x y)) [Bool.true, Bool.true, Bool.false] Bool.false) Bool.false
Test_fold1 = ?
Test_fold2 : Equal (Fold (x => y => (* x y)) [1, 2, 3, 4] 1) 24
Test_fold2 = ?
Test_fold3 : Equal (Fold (x => y => (Concat x y)) [[1], [], [2, 3], [], [4]] [5, 6, 7]) [1, 2, 3, 4, 5, 6, 7]
Test_fold3 = ?Fold_types_different
Note that the type Fold is parameterized by two type variables, x and y, and the parameter f is a binary operator that takes an x and a y and returns a y. Can you think of a situation where it would be useful for x and y to be different?
Functions that build functions
Most of the higher-order functions we've talked about so far use functions as arguments. Let's look at some examples that involve returning functions as results of other functions. To start, here's a function that takes a value x (extracted from some type x) and returns a Nat to x function that returns x every time it's called, ignoring its Nat argument.
Constfun <y> (x: y) : Nat -> y
Constfun x = y => xFtrue : Nat -> Bool
Ftrue = Constfun Bool.trueConstfun_example1 : Equal ((Ftrue) 0n) Bool.true
Constfun_example1 = Equal.reflConstfun_example2 : Equal ((Constfun 5n) 99n) 5n
Constfun_example2 = Equal.reflPlus3 : Nat -> Nat
Plus3 = n => Plus 3n nTest_plus3_1 : Equal ((Plus3) 4n) 7n
Test_plus3_1 = Equal.reflTest_plus3_2 : Equal (Doit3times (Plus3) 0n) 9n
Test_plus3_2 = Equal.reflTest_plus3_3 : Equal (Doit3times (x => Plus 3n x) 0n) 9n
Test_plus3_3 = Equal.reflAdditional Exercises
Many common functions on lists can be implemented in terms of Fold. For example, here's an alternative definition of length:
Fold_length <x> (xs: List x) : Nat
Fold_length xs = Fold (x => y Nat.succ y) xs 0nTest_fold_length1 : Equal (Fold_length [4, 7, 0]) 3n
Test_fold_length1 = Equal.reflProve the validity of Fold_length:
Fold_length_correct <x> (xs: List x) : Equal (Fold_length xs) (List.length xs)
Fold_length_correct xs = ?We can also define Map in terms of Fold. Complete the function:
Fold_map <x> <y> (f: x -> y) (xs: List x) : List y
Fold_map f xs = ?Write a theorem fold_map_correct in Kind stating that Fold_map is correct and prove it:
Fold_map_correct : ?In Kind, a function f: a -> b -> c actually has type a -> (b -> c). That is, if you give f a value of type a, it will provide the function g: b -> c. If you give g a value of type b, it will return a value of type c. This allows for partial application, as in Plus3. Processing a list of arguments with functions that return functions is called currying, in honor of the logician Haskell Curry.
On the other hand, we can reinterpret the function f: a -> b -> c as (Pair a b) -> c. This is called uncurrying. With a binary uncurry function, both arguments must be provided at the same time as a pair; there is no partial application.
We can define curry as follows:
Pair_curry <x> <y> <z> (f: (Pair x y) -> z) (x_val: x) (y_val: y) : z
Pair_curry f x_val y_val = ?As an exercise, define its inverse, Pair_uncurry. Then prove the theorems below to show that the two are inverses.
Pair_uncurry <x> <y> <z> (f: x -> y -> z) (p: Pair x y) : z
Pair_uncurry f p = ?As a (trivial) example of the usefulness of curry, we can use it to shorten one of the examples we saw above:
Test_map2 : Equal (Map (x => Plus 3n x) [2n,0n,2n]) [5n,3n,5n]
Test_map2 = Equal.reflReflection exercise: before executing the following commands, can you calculate the types of Pair_curry and Pair_uncurry?
Uncurry_curry <x> <y> <z> (f: x -> y -> z) (x_val: x) (y_val: y) :
Equal z (Pair_curry (p => Pair_uncurry f p) x_val y_val) (f x_val y_val)
Uncurry_curry f x_val y_val = ?Curry_uncurry <x> <y> <z> (f:(Pair x y) -> z) (p: Pair x y) :
Equal z (Pair_uncurry (x => y => Pair_curry f x y) p) (f p)
Curry_uncurry f p = ?Remember the definition of the function Nth_error(Nth_error_informal):
Nth_error_informal <x> (l: List x) (n: Nat) : Maybe x
Nth_error_informal List.nil n = Maybe.none
Nth_error_informal (List.cons head tail) Nat.zero = Maybe.some head
Nth_error_informal (List.cons head tail) (Nat.succ n) = Nth_error tail nWrite an informal proof of the following theorem:
Nat -> List -> (Equal (Length List) Nat) : Equal (Nth_error_informal List Nat) Maybe.noneWe can explore an alternative way of defining natural numbers, using Church numerals, named after the mathematician Alonzo Church. We can represent a natural number n as a function that takes a function s as a parameter and returns s iterated n times.
Num <x> : Type
Num x = (x -> x) -> x -> xLet's see how to write some numbers with this notation. Iterating a function once should be the same as just applying it. In this way:
One : Num
One = s => z => s z
Note that the function applies an s to a z, if we read the s as successor and the z as zero, we have that One is equal to the successor of zero.
Similarly, Two applies the function s twice to z:
Two : Num
Two = s => z => s (s z)Defining zero is a bit more complicated: how can we "apply a function zero times"? The answer is actually simple: just return the argument untouched.
Zero : Num
Zero = s => z => zMore generally, a number n can be written as s => z => s (s ... (s z) ...), with n occurrences of s. Note in particular how the function doit3times that we defined earlier is actually just the Church representation of 3.
Three : Num
Three = s => z => Doit3times s zComplete the definitions of the following functions. Make sure the corresponding unit tests pass, proving them with Equal.refl.
Successor
Successor of a natural number:
Succ (n: Num) : Num
Succ n = ?
Succ_1 : Equal (Succ Zero) (One)
Succ_1 = ?
Succ_2 : Equal (Succ One) (Two)
Succ_2 = ?
Succ_3 : Equal (Succ Two) (Three)
Succ_3 = ?Addition
Addition of two natural numbers:
Plus (n: Num) (n: Num) : Num
Plus n m = ?
Plus_1 : Equal (Plus One Zero) (One)
Plus_1 = ?
Plus_2 : Equal (Plus Two One) (Plus One Two)
Plus_2 = ?
Plus_3 : Equal (Plus (Plus Two Two) Three) (Plus One (Plus Three Three))
Plus_3 = ?Multiplication
Mult (n: Num) (m: Num) : Num
Mult n m = ?
Mult_1 : Equal (Mult One One) One
Mult_1 = ?
Mult_2 : Equal (Mult Zero (Plus Three Three)) Zero
Mult_2 = ?
Mult_3 : Equal (Mult Two Three) (Plus Three Three)
Mult_3 = ?Exponentiation
It is not possible to make it work with Exp (n: Num) (m: Num) : Num. Polymorphism plays a crucial role here. However, choosing the right type to iterate over can be tricky. If you encounter an "inconsistency" error, try iterating over a different type: Num itself is usually problematic.
Exp (n: Num) (m: Num -> Num) : Num
Exp n m = ?
Exp_1 : Equal (Exp Two Two) (Plus Two Two)
Exp_1 = ?
Exp_2 : Equal (Exp Three Two) (Plus (Mult Two (Mult Two Two)) One)
Exp_2 = ?
Exp_3 : Equal (Exp Three Zero) One
Exp_3 = ?Predecessor
Pred (n: Num -> Num) : Num
Pred n = ?
Pred_1 : Equal (Pred Zero) (Zero)
Pred_1 = ?
Pred_2 : Equal (Pred Two) (One)
Pred_2 = ?
Pred_3 : Equal (Pred Three) (Two)
Pred_3 = ?Subtraction
Sub (n: Num) (m: Num) : Num
Sub n m = ?
Sub_1 : Equal (Sub One Zero) (One)
Sub_1 = ?
Sub_2 : Equal (Sub Two Two) (Sub One One)
Sub_2 = ?
Sub_3 : Equal (Sub Three One) Two
Sub_3 = ?Logic in Kind
In the previous chapters, we saw many examples of factual statements (propositions) and ways to present evidence of their truth (proofs). In particular, we extensively worked with equality propositions in the form e1 = e2, implications (p -> q), and quantified propositions (x -> P(x)). In this chapter, we will see how Kind can be used to perform other familiar forms of logical reasoning.
Before diving into the details, let's talk a little about the status of mathematical statements in Kind. Remember that Kind is a typed language, which means that every meaningful expression in its world has an associated type. Logical statements are no exception: any statement we try to prove in Kind has a type, namely Type, the type of propositions. We can see this with the type Boolean:
Bool: Type
Bool.true : Bool
Bool.false : BoolIn the Bool type we have Bool.true and Bool.false. To create the Bool type, we declare that it is a type (Type) and then that Bool.true and Bool.false are of type Bool. Seeing how it is done, it becomes much simpler. We are often intimidated by the "functional" name, but Kind is a very friendly language, we will see more about this later on.
Another possible example is Nat, the natural numbers. Natural numbers are all non-negative integers. That is, they start with the number zero and go to infinity, but do not have decimal values. Therefore, 3 is a natural number, but 3.14 is not, just as -3 is not. So we know that the natural number is made up of zero and its successors. Let's see how this is in Kind:
Nat: Type
Nat.zero : Nat
Nat.succ (pred: Nat) : NatWe notice that the construction is similar to Booleans, but there is an extra element in Nat.succ, which is "(pred: Nat)", and this is because, while in the other we had only two return options (True or False), now we have an infinity of numbers that the code needs to understand, and there must be a way for the code to stop running (we will see more about this throughout this study), since code that never stops running is code that will never give us the result.
However, in any case, we notice that the structure of Nat is basically the same as Bool, which shows us that we can create any type, as long as we follow the same structure. Let's create the juice type:
Juice : Type
Juice.orange : Juice
Juice.cashew : JuiceOrange juice has two constructors, Juice.orange and Juice.cashew. This type is fictitious, it did not exist until now, but now we can use it as a type and this shows us that, thanks to Kind's design, we can create an infinity of types, since every type is a function.
Understanding the construction of types will prevent some syntax errors from occurring.
to review, our element Juice is of type Type and Juice.orange is of type Juice. Thus, in layman's terms, the element is to the right of the colon and the type is to the left:
element : TypeAs previously mentioned, even types are functions, so we can have a function as a type. For example:
Problem : Equal Bool Bool.true Bool.trueWe can see that we have an element called "Problem" and it is of type "(Equal Bool Bool.true Bool.true)". We have seen this structure several times in the past chapters, and it is now easy to understand that this function is a type and, just as we don't write it, we cannot simply copy the function to the constructors of this type.
Juice: Type
Juice.orange : TypeJuice is of type Type, but Juice.orange is not of type Type, it is of type Juice.
But be aware that all syntactically well-formed propositions have type Type in Kind, regardless of whether they are true or not. Simply being a proposition is one thing; being demonstrable is another thing!
In fact, propositions do not just have types: they are first-class objects that can be manipulated in the same way as other entities in the world of Kind. So far, we have seen a primary location where propositions can appear: in the type signatures of functions.
Plus_2_2_is_4 : Equal (Plus 2n 2n) 4n
Plus_2_2_is_4 = Equal.reflBut propositions can be used in many other ways. For example, we can give a name to a proposition as a value in its own right, just as we gave names to expressions of other types.
Plus_fact : Type
Plus_fact = Equal (Plus 2n 2n) 4nLater, we can use this name in any situation where a proposition is expected - for example, in a function declaration.
Plus_fact_is_true : Plus_fact
Plus_fact_is_true = Equal.reflWe can also write parameterized propositions - that is, functions that take arguments of some type and return a proposition. For example, the following function takes a number and returns a proposition asserting that this number is equal to three:
Is_three (n: Nat) : Type
Is_three n = Equal Nat n 3nIn Kind, functions that return propositions are said to define properties of their arguments. For example, here is a (polymorphic) property that defines the familiar notion of an injective function:
Injective <a> <b> (f: a -> b) : Type
Injective a b f = (x: a) -> (y: a) -> (e: Equal b (f x) (f y)) -> (Equal a x y)We can instantiate a rule of injectivity with
Nat.succ_injective : Injective ((x: Nat) => Nat.succ x)
Nat.succ_injective =
(a: Nat) =>
(b: Nat) =>
(e: Equal Nat (Nat.succ a) (Nat.succ b)) =>
Equal.apply (x => Nat.pred x) eLogical Connectives
Conjunction
The conjunction (logical "and") in kind takes two propositions a and b, which should return a Boolean value true or false.
Bool.and (a: Bool) (b: Bool) : Bool
Bool.and Bool.true b = b
Bool.and Bool.false b = Bool.falseIf a is true, it is sufficient to return the value of b. However, if a is false, there is no need to verify the value of the second element.
Because it is a limited case (there are only two options), it is possible to verify with a simple proof:
ConjunctiveBool : Equal Bool (Bool.and Bool.true Bool.false) Bool.false
ConjunctiveBool = Equal.reflAnd_exercise
And_exercise : Pair (Equal (Plus 3n 4n) 7n) (Equal (Mult 2n 2n) 4n)
And_exercise = ?Both for proving conjunctive statements. To go in the other direction – that is, to use a conjunctive hypothesis to help prove something else – we employ pattern matching.
If the proof context contains a hypothesis h of the form (a,b), the case division will replace it with a pattern of pairs (a,b).
And_example2 (n: Nat) (m: Nat) (e: Pair (Equal n 0n) (Equal m 0n)) : Equal (Plus n m ) 0n
And_example2 Nat.zero Nat.zero e = Equal.refl
And_example2 Nat.zero (Nat.succ m ) e =
let p = (Equal.rewrite
(Pair.snd e)
(x => match Nat x {
zero => Empty
succ => Unit
})
(Unit.new))
Empty.absurd p
And_example2 (Nat.succ n) m e =
let p = (Equal.rewrite
(Pair.fst e)
(x => match Nat x {
zero => Empty
succ => Unit
})
(Unit.new))
Empty.absurd pYou may wonder why we bother to group the two hypotheses n = 0 and m = 0 into a single conjunction, since we could also have declared the theorem with two separate premises:
And_example2a (n: Nat) (m: Nat) (e1: Equal n 0n) (e2: Equal m 0n) : Equal (Plus n m) 0n
And_example2a Nat.zero Nat.zero e1 e2 = Equal.refl
And_example2a Nat.zero (Nat.succ m ) e1 e2 =
let p = (Equal.rewrite
(e2)
(x => match Nat x {
zero => Empty
succ => Unit
})
(Unit.new))
Empty.absurd p
And_example2a (Nat.succ n) m e1 e2 =
let p = (Equal.rewrite
(e1)
(x => match Nat x {
zero => Empty
succ => Unit
})
(Unit.new))
Empty.absurd p
For this theorem, both formulations are adequate. But it is important to understand how to work with conjunctive hypotheses because conjunctions often arise from intermediate steps in proofs, especially in larger developments. Here is a simple example:
And_example3 (n: Nat) (m: Nat) (e: Equal (Plus n m) 0n) : Equal (Mult n m) 0n
And_example3 Nat.zero m e = Equal.refl
And_example3 (Nat.succ n) m e =
let p = (Equal.rewrite
(e)
(x => match Nat x {
zero => Empty
succ => Unit
})
(Unit.new))
Empty.absurd pAnother common situation with conjunctions is that we know (a,b), but in some context we need only a (or only b). The following theorems are useful in such cases:
Proj1 <p> <q> (a: Pair p q) : p
Proj1 (Pair.new fst snd) = fstProj2
Proj2 <p> <q> (b: Pair p q) : q
Proj2 (Pair.new fst snd) = ?Finally, sometimes we need to rearrange the order of the conjunctions and/or group the conjunctions of multiple paths. The following commutativity and associativity theorems are useful in such cases.
And_commut <p> <q> (c: Pair p q) : Pair q p
And_commut (Pair.new fst snd) = Pair.new snd fstAnd_assoc
And_assoc <p> <q> <r> (a: Pair p (Pair q r)) : Pair (Pair p q) r
And_assoc (Pair.new p (Pair q r) fst (Pair.new snd trd)) = ?Disjunction
Another important connective is the disjunction, or logical "or", of two propositions:
Either a b is true when either a or b is true. The first case was marked with left, and the second with right.
To use a disjunctive hypothesis in a proof, we proceed by case analysis, which, as for Nat or other data types, can be done with pattern matching. Here is an example:
Or_example (n: Nat) (m: Nat) (e: (Either (Equal n 0n) (Equal m 0n))) : Equal (Mult n m) 0n
Or_example Nat.zero m e = Equal.refl
Or_example n Nat.zero e = Mult_0_r n
Or_example (Nat.succ n) m (Either.left l r val) =
let p = (Equal.rewrite
(val)
( x => match Nat x {
zero => Empty
succ => Unit
})
(Unit.new))
Empty.absurd p
Or_example (Nat.succ n) (Nat.succ m) (Either.right l r val) =
let p = (Equal.rewrite
(val)
( x => match Nat x {
zero => Empty
succ => Unit
})
(Unit.new))
Empty.absurd pConversely, to show that a disjunction is valid, we need to show that one of its sides is valid. This can be done through the Left and Right constructors mentioned above. Here is a trivial use...
#axiom
Or_intro_left <a> <b> (t: a) : Either a b
Or_intro_left t = Either.left t
#axiom
Or_intro_right <a> <b> (t: b) : Either a b
Or_intro_right t = Either.right t... and a slightly more interesting example requiring both.
Zero_or_succ (n: Nat) : Either (Equal n 0n) (Equal n (Nat.succ (Nat.pred n)))
Zero_or_succ Nat.zero = Either.left Equal.refl
Zero_or_succ (Nat.succ n) = Either.right Equal.reflMult_eq_0
#axiom
Mult_eq_0 (n: Nat) (m: Nat) (e: Equal (Mult n m) 0n) : Either (Equal n 0n) (Equal m 0n)
Mult_eq_0 n m e = ?Or_commut
Or_commut <p> <q> (e: Either p q) : Either q p
Or_commut e: ?Falsehood and Negation
Up until now, we have mainly been concerned with proving that certain things are true - addition is commutative, list concatenation is associative, etc. Of course, we may also be interested in negative results, showing that certain propositions are not true. In Kind, such negative statements are expressed with the negation type-level function Not.
To see how negation works, recall the discussion of the principle of explosion from the previous chapter; it states that if we assume a contradiction, then any other proposition can be derived. Following this intuition, we could define Not p as q -> (p -> q). Kind actually makes a slightly different choice, defining Not as p -> Empty, where Empty is a specific contradictory proposition defined in the standard library as a data type with no constructors.
Empty: Type
Not <p: Type>: Type
Not p = p -> EmptySince Empty is a contradictory proposition, the principle of explosion also applies to it. If we obtain Empty in the proof context, we can call it Empty or absurd to complete any goal:
Ex_falso_quodlibet <p> : Empty -> p
Ex_falso_quodlibet p = e => Empty.absurd eThe Latin phrase ex falso quodlibet literally means "from falsehood, anything follows"; this is another common name for the principle of explosion.
Not_implies_our_not
Show that the definition of negation in Kind implies the intuitive one mentioned above:
Not_implies_our_not <p> <q> (e: Not p) : q -> (p -> q)
Not_implies_our_not p q e = ?This is how we use Not to assert that 0 and 1 are different elements of Nat:
Zero_not_one : Not (Equal Nat.zero (Nat.succ Nat.zero))
Zero_not_one =
(emp =>
let app = Equal.apply (x => Nat.is_zero x) emp
Equal.rewrite app (e => if e {Nat} else {Empty}) Nat.zero)It takes a bit of practice to get used to working with negation in Kind. Even if you can see perfectly well why a statement involving negation is true, it can be a bit tricky at first to get things set up in the right way so that Kind can understand! Here are proofs of some familiar facts to warm you up:
Not_false : Not Empty
Not_false = e => Empty.absurd e
Contradiction_implies_anything <p> <q> (a: Pair p (Not p)) : q
Contradiction_implies_anything p q (Pair.new fst snd) =
let app = snd fst
Empty.absurd app
Double_neg_inf
Write an informal proof of Double_neg:
Theorem: If p, then (not (not p)), for any proposition p.
Contrapositive
Contrapositive <p> <q> (f: p -> q) : (Not q -> Not p)
Contrapositive p q f = ?Not_both_true_and_false
Not_both_true_and_false <p> : Not (Pair p (Not p))
Not_both_true_and_false p = ?Similarly, since inequality involves negation, it takes a bit of practice to work with it fluently. Here's a useful trick. If you're trying to prove a goal that is absurd (e.g., the final state is Bool.false = Bool.true), apply Empty.absurd to change the goal to Empty. This makes it easier to use assumptions of the form (Not p) that may be available in the context - in particular, assumptions of the form Not (x = y).
Not_true_is_false (b: Bool) (e: Not (Equal Bool b Bool.true)) : Equal Bool b Bool.false
Not_true_is_false Bool.false e = Equal.refl
Not_true_is_false Bool.true e = Empty.absurd (e Equal.refl)Truth
In addition to Empty, the standard library of Kind also defines Unit, a proposition that is trivially true. To prove this, we use the constant:
True_is_true : Unit
True_is_true = Unit.newUnlike Empty, which is widely used, Unit is rarely used in proofs since it is trivial (and therefore uninteresting) to prove as a goal and carries no useful information as a hypothesis. However, it can be quite useful when defining complex proofs using conditionals or as a parameter for higher-order proofs. We will see examples of this use of Unit later.
Logical Equivalence
Logical Equivalence. The useful connective "if and only if", which asserts that two propositions have the same truth value, is just the conjunction of two implications.
record Equivalence (p: Type) (q: Type) {
lft: p -> q
rgt: q -> p
}Equivalence.lft <p> <q> (e: Equivalence p q) : p
Equivalence.lft (Equivalence.new l r) = r (Equivalence.rgt (Equivalence.new l r))
Equivalence.rgt <p> <q> (e: Equivalence p q) : q
Equivalence.rgt (Equivalence.new l r) = l (Equivalence.lft (Equivalence.new l r))Not_true_iff_false (b: Bool) : Equivalence (Not (Equal Bool b Bool.true)) (Equal Bool b Bool.false)
Not_true_iff_false b = Equivalence.new (x => Not_true_is_false b x) (y => Not_true_and_false b y)Not_true_and_false (b : Bool) (e: Equal Bool b Bool.false) : Not (Equal Bool b Bool.true)
Not_true_and_false Bool.false Equal.refl =
emp =>
let p = Equal.rewrite emp
(x => match Bool x {
true => Empty
false => Unit
})
(Unit.new)
Empty.absurd p
Not_true_and_false Bool.true e =
let p = Equal.rewrite e
(x => if x
{Unit}
else
{Empty})
(Unit.new)
Empty.absurd pSymmetry
A relation is symmetric if, for all elements p and q in its domain, if p is equivalent to q, then q is equivalent to p. This can be proved with the following rule:
Equivalence.mirror <p> <q> (e: Equivalence p q) : Equivalence q p
Equivalence.mirror p q (Equivalence.new lft rgt) = (Equivalence.new rgt lft)Reflexivity
A relation is reflexive if, for every element p in its domain, p is equivalent to itself. This can be proved with the following rule:
Equivalence.refl <p> : Equivalence p p
Equivalence.refl p = ?Transitivity
A relation is transitive if, for all elements p, q, and r in its domain, if p is equivalent to q and q is equivalent to r, then p is equivalent to r. This can be proved with the following rule:
Equivalence.chain <p> <q> <r> (e0: Equivalence p q) (e1: Equivalence q r) : Equivalence p r
Equivalence.chain p q r e0 e1 = ?Or_distributes_over_and
Or_distributes_over_and <p> <q> <r> : Equivalence (Either p (Pair q r)) (Pair (Either p q) (Either p r))
Or_distributes_over_and p q r = ?A special form of equivalence, avoiding the need for some low-level proof state manipulation. In particular, rewrite and reflexivity can be used with iff assertions, not just equalities. Here's a simple example demonstrating how these tactics work with iff. First, let's prove some basic iff equivalences:
Mult_0 (n: Nat) (m: Nat) : Equivalence (Equal Nat (Mult n m) 0n) (Either (Equal Nat n 0n) (Equal Nat m 0n))
Mult_0 n m = Equivalence.new (x => To_mult_0 n m x) (y => Or_example n m y)
To_mult_0 (n: Nat) (m: Nat) (e: Equal Nat (Mult n m) 0n) : (Either (Equal Nat n 0n) (Equal Nat m 0n))
To_mult_0 Nat.zero Nat.zero Equal.refl = Either.right Equal.refl
To_mult_0 Nat.zero (Nat.succ m) Equal.refl = Either.left Equal.refl
To_mult_0 (Nat.succ n) Nat.zero e = Either.right Equal.refl
To_mult_0 (Nat.succ n) (Nat.succ m) e =
let a = Plus_comm (Mult n (Nat.succ m)) (Nat.succ m)
let b = Equal.chain (Equal.mirror e) a
let c = (Equal.rewrite b
(x => match Nat x {
zero => Unit
succ => Empty
})
(Unit.new))
Empty.absurd cOr_assoc <p> <q> <r> : Equivalence (Either p (Either q r)) (Either (Either p q) r)
Or_assoc = Equivalence.new (x => To_or_assoc x) (y => Fro_or_assoc y)
To_or_assoc <p> <q> <r> (e: Either p (Either q r)) : Either (Either p q) r
To_or_assoc (Either.left e) = Either.left (Either.left e)
To_or_assoc (Either.right p (Either q r) (Either.left e)) = Either.left (Either.right e)
To_or_assoc (Either.right p (Either q r) (Either.right e)) = Either.right e
Fro_or_assoc <p> <q> <r> (e: Either (Either p q) r) : Either p (Either q r)
Fro_or_assoc (Either.left (Either p q) r (Either.left e)) = Either.left e
Fro_or_assoc (Either.left (Either p q) r (Either.right e)) = Either.right (Either.left e)
Fro_or_assoc (Either.right (Either p q) r e) = Either.right (Either.right e)Now we can use these facts with Equal.rewrite and Equal.refl to provide smooth proofs of assertions involving equivalences. Here's a ternary version of the previous result of Mult_0:
Mult_0_3 (n: Nat) (m: Nat) (p: Nat) : Equivalence (Equal Nat (Mult n (Mult m p)) 0n) (Either (Equal Nat n 0n) (Either (Equal Nat m 0n) (Equal Nat p 0n)))
Mult_0_3 n m p = Equivalence.new (x => To_mult_0_3 n m p x) (y => Fro_mult_0_3 n m p y)
To_mult_0_3 (n: Nat) (m: Nat) (p: Nat) (e: (Equal Nat (Nat.mul n (Nat.mul m p)) 0n)) : (Either (Equal Nat n 0n) (Either (Equal Nat m 0n) (Equal Nat p 0n)))
To_mult_0_3 n m p e = Either.swap (Equivalence.rgt (Or_assoc (Equal m 0n) (Equal p 0n) (Equal n 0n)))
Fro_mult_0_3 (n: Nat) (m: Nat) (p: Nat) (e: Either (Equal Nat n 0n) (Either (Equal Nat m 0n) (Equal Nat p 0n))) : (Equal Nat (Mult n (Mult m p)) 0n)
Fro_mult_0_3 (n: Nat) (m: Nat) (p: Nat) (e: Either (Equal Nat n 0n) (Either (Equal Nat m 0n) (Equal Nat p 0n))) : (Equal Nat (Nat.mul n (Nat.mul m p)) 0n)
Fro_mult_0_3 Nat.zero m p (Either.left Equal.refl) = Equal.refl
Fro_mult_0_3 n Nat.zero p (Either.right a (Either b c) (Either.left Equal.refl)) = Mult_comm 0n n
Fro_mult_0_3 n m Nat.zero (Either.right a (Either b c) (Either.right Equal.refl)) = Equal.chain (Mult_assoc n m 0n) (Mult_0_r (Nat.mul n m))
Fro_mult_0_3 (Nat.succ n) m p (Either.left e) =
let p = (Equal.rewrite
e
(x => match Nat x {
zero => Empty
succ => Unit
})
(Unit.new))
Empty.absurd p
Fro_mult_0_3 n (Nat.succ m) p (Either.right a (Either b c) (Either.left e)) =
let p = (Equal.rewrite
e
(x => match Nat x {
zero => Empty
succ => Unit
})
(Unit.new))
Empty.absurd p
Fro_mult_0_3 n m (Nat.succ p) (Either.right a (Either b c) (Either.right e)) =
let p = (Equal.rewrite
e
(x => match Nat x {
zero => Empty
succ => Unit
})
(Unit.new))
Empty.absurd pThe apply tactic can also be used with equivalence. When given an equivalence as its argument, apply tries to guess which side of the equivalence to use.
Apply_iff_example (n: Nat) (m: Nat) (e: Equal Nat (Mult n m) 0n) : Either (Equal Nat n 0n) (Equal Nat m 0n)
Apply_iff_example n m e = Equivalence.rgt (Mult_0 n m)
Existential Quantification
Another important logical connective is existential quantification. To say that there is some x of type Type such that some property p is true for x, we write (Sigma x p).
record Sigma (x: Type) (p: x -> Type) {
fst : x
snd : (p fst)
}- Currently, the Kind-lang has a compiler bug that is affecting the lambda application of Sigma.
To prove a statement of the form (Sigma x p), we must show that p is true for some specific choice of value for x, known as the existential witness. This is done in two steps: First, we explicitly inform Kind of the witness x we have in mind by writing it in the first parameter. Then, we prove that p is true after all occurrences of x are replaced with Type.
Four_is_even : Sigma Nat (n => (Equal Nat 4n (Nat.add n n)))
Four_is_even = $ 2n Equal.reflOn the other hand, if we have an existential hypothesis (Sigma x p) in the context, we can pattern match on it to obtain a witness x and a hypothesis asserting that p is true for x.
Exists_example_2 (n: Nat) (m: Sigma Nat (m => (Equal Nat n (Nat.add 4n m)))) : Sigma Nat (o => (Equal Nat n (Nat.add 2n o)))
Exists_example_2 n (Sigma.new Nat s fst snd) = Sigma.new fst ?Dist_not_exists
Prove that "p is true for all x" implies "there is no x for which p is not true"
Dist_not_exists <a> <p: a -> Type> (f: (x: a) -> (p x)) : Not (Sigma a (x => ( Not (p x))))
Dist_not_exists a p f = ?Dist_exists_or
Prove that existential quantification distributes over disjunction.
Dist_exists_or <a> <p: a -> Type> <q: a -> Type> : Equivalence (Sigma a (x => (Either (p x) (q x)))) (Either (Sigma a (x => (p x))) (Sigma a (x => (q x))))
Dist_exists_or a p q = ?dist_exists_or_rhsPropositional programming
The logical connectives we have seen provide a rich vocabulary for defining complex propositions from simpler ones. To illustrate, let's see how to express the statement that an element x occurs in a List l. Note that this property has a simple recursive structure:
- If l is the empty list, then x cannot occur in it, so the property "x appears in l" is simply false.
- Otherwise, l has the form List.cons head tail. In this case, x occurs in l if it is equal to head or if it occurs in tail.
We can translate this directly into a simple recursive function that takes an element and a List and returns a proposition:
In <a> (x: a) (l: List a) : Type
In a x List.nil = Empty
In a x (List.cons head tail) = Either (Equal a x head) (In a x tail) When In is applied to a concrete list, it expands into a concrete sequence of nested disjunctions.
In_example_1 : In 4n [1n, 2n, 3n, 4n, 5n]
In_example_1 = (Either.right (Either.right (Either.right (Either.left Equal.refl))))
In_example_2 (n: Nat) (i: In n [2n, 4n]) : Sigma Nat (m => Equal Nat n (Nat.mul 2n m))
In_example_2 n (Either.left e) = $ 1n e
In_example_2 n (Either.right l (Either rl rr) (Either.left e)) = $ 2n e
In_example_2 n (Either.right l (Either rl rr) (Either.right e)) = Empty.absurd eWe can also prove more generic and higher-level lemmas about In. Note, in the next example, how In starts being applied to a variable and is only expanded when we do case analysis on that variable:
In_map <a> <b> (f: a -> b) (l: List a) (x: a) (i: In x l) : In (f x) (List.map l f)
In_map a b f (List.nil) x i = Empty.absurd i
In_map a b f (List.cons head tail) x (Either.right e) = Either.right (In_map f tail x e)
In_map a b f (List.cons head tail) x (Either.left e) =
(Equal.rewrite e
(y => (Either (Equal (f x) (f y)) (In (f x) (List.map tail f))))
(Either.left Equal.refl))This way of defining propositions recursively, while convenient in some cases, also has some disadvantages. In particular, it is subject to the usual Kind restrictions on the definition of recursive functions, for example, the requirement that they be "obviously terminating". In the next chapter, we will see how to define propositions inductively, a different technique with its own set of strengths and limitations.
In_map_equiv
In_map_equiv <a> <b> (f: a -> b) (l: List a) (y: b) :
Equivalence (In y (List.map l f)) (Sigma a (x => (Pair (Equal (f x) y) (In x l))))
In_map_equiv a b f l y = ?In_app_equiv
In_app_equiv <a> (x: a) (l1: List a) (l2: List a) :
(Equivalence (In x (List.concat l1 l2)) (Either (In x l1) (In x l2)))
In_app_equiv a x l1 l2 = ?All
Remember that functions that return propositions can be seen as properties of their arguments. For example, if p has type Nat -> Type, then p n asserts that the property p is true for n.
Inspired by In, write a recursive function All asserting that some property p is true for all elements of a List l. To ensure that your definition is correct, prove the lemma All_In below. (Of course, your definition should not just repeat the left-hand side of All_In.)
All <t> (p: t -> Type) (l: List t) : Type
All t p l = ?
All_in <t> (p: t -> Type) (l: List t) : Equivalence ((x: t) -> (i: In x l) -> p x) (All p l)
All_in t p l = ?Combine_odd_even
Complete the definition of the function combine_odd_even below. It takes as arguments two properties of numbers, podd and peven, and should return a property p such that p n is equivalent to podd n when n is odd and equivalent to peven n otherwise
Combine_odd_even (podd: Nat -> Type) (peven: Nat -> Type) : Nat -> Type
Combine_odd_even podd peven = ?To test your definition, prove the following theorems:
Combine_odd_even_intro
(n: Nat)
(podd: Nat -> Type)
(peven: Nat -> Type)
(p1: (Equal (Nat.is_odd n) Bool.true) -> podd n)
(p2: (Equal (Nat.is_odd n) Bool.false) -> peven n) : (Combine_odd_even (podd) (peven)) n
Combine_odd_even_intro n podd peven p1 p2 = ?
Combine_odd_even_elim_odd
(n: Nat)
(podd: Nat -> Type)
(peven: Nat -> Type)
(p: (Combine_odd_even podd peven) n)
(e: Equal (Nat.is_odd n) Bool.true) : podd n
Combine_odd_even_elim_odd n podd peven p e = ?
Combine_odd_elim_even
(n: Nat)
(podd: Nat -> Type)
(peven: Nat -> Type)
(p: (Combine_odd_even podd peven) n)
(e: Equal (Nat.is_odd n) Bool.false) : peven n
Combine_odd_elim_even n podd peven p e = ?Applying Theorems to Arguments
A characteristic of Kind that distinguishes it from many other proof assistants is that it treats proofs as first-class objects.
There is much to be said about this, but it is not necessary to understand in detail to use Kind. This section offers only a sample, while a deeper exploration can be found in the ProofObjects chapter.
We saw that we can use the check command to ask Kind to print the type of an expression. We can also use check to ask which theorem a particular identifier refers to.
PlusCommutative (m: Nat) (n: Nat) : Equal (Nat.add n m) (Nat.add m n)
PlusCommutative m n = ?Kind prints the statement of the plusCommutative theorem in the same way it prints the type of any term we ask it to check. Why?
The reason is that the identifier plusCommutative actually refers to a proof object - a data structure that represents a logical derivation establishing the truth of the statement (n: Nat) (m: Nat) : n + m = m + n. The type of this object is the statement of the theorem of which it is a proof. Intuitively, this makes sense because the statement of a theorem tells us what we can use it for, just as the type of a computational object tells us what we can do with that object - for example, if we have a term of type Nat -> Nat -> Nat, we can give it two Nats as arguments and get a Nat back. Similarly, if we have an object of type n = m -> n + n = m + m and provide it with an "argument" of type n = m, we can derive n + n = m + m. Operationally, this analogy goes even further: by applying a theorem, as if it were a function, to hypotheses with corresponding types, we can specialize its result without having to resort to intermediate assertions. For example, suppose we wanted to prove the following result:
Plus_comm3a: (n: Nat) (m: Nat) (p: Nat) : Equal (Nat.add n (Nat.add m p)) (Nat.add (Nat.add p m) n)At first glance, it seems like we should be able to prove this by case analysis, for the zero and succ _ cases, but that would give us unnecessary work. Let's see an example:
Plus_comm3a Nat.zero n p = ?In this case, our goal is to prove:
(Equal _ (Nat.add n p) (Nat.add (Nat.add p 0n) n))
But notice, for this we need another proof, that of
Equal Nat (Nat.add p 0n) p
To prove this, we would take the following steps:
Add_n_z (n: Nat) : (Equal (Nat.add n Nat.zero) n)
Add_n_z Nat.zero = Equal.refl
Add_n_z (Nat.succ n) =
let ind = Add_n_z n
let app = (Equal.apply (x => (Nat.succ x)) ind)
appNow let's prove:
Plus_comm3a (n: Nat) (m: Nat) (p: Nat) : Equal (Nat.add n (Nat.add m p)) (Nat.add (Nat.add p m) n)
Plus_comm3a Nat.zero n p =
let pzr = Add_z_r p
let com = Plus_comm n p
let rwt = Equal.rewrite (Equal.mirror pzr) (x =>(Equal _ (Nat.add n p) (Nat.add (x) n))) com
rwtNow we only need to prove it for the case of Nat.succ n
Plus_comm3a (Nat.succ m) n p = ?and our goal is (Equal _ (Nat.succ (Nat.add m (Nat.add n p))) (Nat.add (Nat.add p n) (Nat.succ m))) and for that we would need other proofs, such as the one that
Plus_n_sm (n: Nat) (m: Nat) : (Equal Nat (Nat.succ (Nat.add n m))(Nat.add n (Nat.succ m)))
Plus_n_sm Nat.zero m = Equal.refl
Plus_n_sm (Nat.succ n) m = (Equal.apply (x => (Nat.succ x)) (Plus_n_sm n m))And rewrite in the proof of the commutativity of addition between n and p and then use the proof of commutativity for all of this, a tiring and, I can say, unnecessary job.
Instead of doing case analysis, let's work with them as pure variables, almost without value
Plus_comm3 (m: Nat) (n: Nat) (p: Nat) : Equal (Nat.add n (Nat.add m p)) (Nat.add (Nat.add p m) n)
Plus_comm3 m n p = ?Our goal remains (Equal _ (Nat.add n (Nat.add m p)) (Nat.add (Nat.add p m) n)) and to understand this, let's analyze our problem and the next steps will be too trivial:
- n + (m + p) = (p + m) + n
This is exactly the commutativity of addition, so we just need to rewrite our Plus_comm proof twice, one inside the other
let a = Equal.rewrite (Plus_comm p m) (x => (Equal (Nat.add n (Nat.add m p)) (Nat.add (x) n))) (Plus_comm3 m n p)and see what our variable a returns
(Equal Nat (Nat.add n (Nat.add m p)) (Nat.add (Nat.add m p) n))
We're almost there, we just need to rewrite the second Plus_comm in the innermost addition on the right-hand side
let b = Equal.rewrite (Plus_comm m p) (x => (Equal Nat (Nat.add n (Nat.add m p)) (Nat.add (x) n))) aand our b is exactly equal to our goal
(Equal Nat (Nat.add n (Nat.add m p)) (Nat.add (Nat.add p m) n))
The complete proof is:
Plus_comm3 (m: Nat) (n: Nat) (p: Nat) : Equal (Nat.add n (Nat.add m p)) (Nat.add (Nat.add p m) n)
Plus_comm3 m n p =
let a = Equal.rewrite (Plus_comm p m) (x => (Equal (Nat.add n (Nat.add m p)) (Nat.add (x) n))) (Plus_comm3 m n p)
let b = Equal.rewrite (Plus_comm m p) (x => (Equal Nat (Nat.add n (Nat.add m p)) (Nat.add (x) n))) a
bMuch simpler and more elegant, it didn't require so much work, a brief reading of the problem practically gave us the solution. Notice that this was no different from everything we have done so far, it is even a repetition of the previous steps, it is similar to the application of a polymorphic function to an argument of type.
You can "use theorems as functions" in this way with almost all tactics that receive a theorem name as an argument. Note also that theorem application uses the same inference mechanisms as function application; therefore, it is possible, for example, to provide wildcards as arguments to be inferred, or declare some hypotheses of a theorem as implicit by default. These features are illustrated in the proof below.
Kind vs Set Theory
The logical core of Coq, the Calculus of Inductive Constructions, differs in some important ways from other formal systems used by mathematicians to write precise and rigorous proofs. For example, in the most popular foundation for mathematics in conventional pen-and-paper, Zermelo-Fraenkel set theory (ZFC), a mathematical object can potentially be a member of many different sets; a term in Kind's logic, on the other hand, is a member of at most one type. This difference often leads to slightly different ways of capturing informal mathematical concepts, but these are largely quite natural and easy to work with. For example, instead of saying that a natural number n belongs to the set of even numbers, we would say in Kind that ev n is true, where ev: Nat -> Type is a property that describes even numbers.
However, there are some cases where translating standard mathematical reasoning to Kind can be both laborious and sometimes even impossible, unless we enrich the core logic with additional axioms. We conclude this chapter with a brief discussion of some of the most significant differences between the two worlds.
Functional Extensionality
The equality statements we have seen so far mainly concern elements of inductive types (Nat, Bool, etc.). But since Kind's equality operator is polymorphic, these are not the only possibilities -- in particular, we can write propositions that assert that two functions are equal to each other:
#![allow(unused)] fn main() { Function_equality_ex1 : Equal (Nat.succ 3n) (Nat.succ (Nat.pred 4n)) Function_equality_ex1 = Equal.refl }
In common mathematical practice, two functions f and g are considered equal if they produce the same outputs:
(∀𝑥, 𝑓(𝑥) = 𝑔(𝑥)) → 𝑓 = 𝑔
This is known as the principle of functional extensionality.
Informally, an "extensional property" is one that concerns the observable behavior of an object. Thus, functional extensionality simply means that the identity of a function is completely determined by what we can observe from it -- that is, in terms of Kind, the results we obtain after applying it.
Functional extensionality is not part of Kind's basic axioms. This means that some "reasonable" propositions are not provable.
#![allow(unused)] fn main() { Function_equality_ex2 : Equal ((x: Nat) => Nat.add x 1n) ((x: Nat) => Nat.add 1n x) Function_equality_ex2 = ? }
However, we can state a theorem and skip its proof or use a hole.
#![allow(unused)] fn main() { Functional_extensionality <a><b> (f: a -> b) (g: a -> b) (e: (x: a) -> Equal (f x) (g x)) : Equal f g }
Now we can invoke functional extensionality in proofs:
#![allow(unused)] fn main() { Function_equality_ex2 : Equal ((x: Nat) => Nat.add x 1n) ((x: Nat) => Nat.add 1n x) Function_equality_ex2 = Functional_extensionality ((x: Nat) => Nat.add x 1n) ((x: Nat) => Nat.add 1n x) (x => Plus_comm x 1n) }
Of course, we should be careful when adding new axioms to Kind's logic, as they may make it inconsistent -- that is, they may make it possible to prove all propositions, including Empty!
Unfortunately, there is no simple way to tell whether an axiom is safe to add: it usually takes hard work to establish the consistency of any particular combination of axioms.
However, it is known that adding functional extensionality, in particular, is consistent.
Tr_rev
A problem with the definition of the list reversal function "rev" we have is that it performs a call to "++" at each step. Executing "++" takes asymptotically linear time in the size of the list, which means that "rev" has quadratic running time. We can improve this with the following definition:
#![allow(unused)] fn main() { Rev_append <x> (l1: List x) (l2: List x) : List x Rev_append x List.nil l2 = l2 Rev_append x (List.cons xs.h xs.t) l2 = Rev_append xs.t (List.cons xs.h l2) Tr_rev <x> (l: List x) : List x Tr_rev x l = Rev_append x l List.nil1 }
This version is said to be tail-recursive, because the recursive call to the function is the last operation that needs to be performed (i.e., we don't need to execute ++ after the recursive call); a decent compiler will generate very efficient code in this case. Prove that the two definitions are actually equivalent.
#![allow(unused)] fn main() { Tr_rev_correct <a> (xs: List a) : Equal (Tr_rev xs) (Rev xs) Tr_rev_correct a xs = ? }
Propositions and Booleans
We have seen two different ways of encoding logical facts in Kind: with booleans (of type Bool) and with propositions (of type Type).
For example, to assert that a number n is even, we can say that • (1) evenb n returns True, or • (2) there exists a k such that n = double k. In fact, these two notions of parity are equivalent, as can be easily shown with a pair of auxiliary lemmas.
We often say that the boolean evenb n reflects the proposition (n => Equal n (double k)).
#![allow(unused)] fn main() { Evenb_double (k: Nat) : Equal (Nat.is_even (Nat.double k)) Bool.true Evenb_double Nat.zero = Equal.refl Evenb_double (Nat.succ k) = Evenb_double k }
Evenb_double_conv
#![allow(unused)] fn main() { Evenb_double_conv (n: Nat): Sigma Nat (k => (Equal n (Bool.if (Evenb n) (Nat.double k) (Nat.succ (Nat.double k))))) Evenb_double_conv n = ? }
#![allow(unused)] fn main() { Even_bool_prop (n: Nat): Equivalence (Equal (Evenb n) Bool.true) (Sigma Nat (k => Equal n (Nat.double k))) }
Similarly, to assert that two numbers n and m are equal, we can say (1) that n == m returns Bool.true or (2) that n = m. These two notions are equivalent.
#![allow(unused)] fn main() { Beq_nat_true_equiv (n1: Nat) (n2: Nat) : Equivalence (Equal (Nat.equal n1 n2) Bool.true) (Equal n1 n2) Beq_nat_true_equiv n1 n2 = Equivalence.new (x => To_beq_nat_true n1 n2 x) (y => Fro_beq_nat_true n1 n2 y) To_beq_nat_true (n1: Nat) (n2: Nat) (e: Equal (Nat.equal n1 n2) Bool.true) : Equal n1 n2 To_beq_nat_true Nat.zero Nat.zero Equal.refl = Equal.refl To_beq_nat_true Nat.zero (Nat.succ n2) e = let emp = (Equal.rewrite e (x => match Bool x { true => Empty false => Unit }) (Unit.new)) Empty.absurd emp To_beq_nat_true (Nat.succ n1) Nat.zero e = let emp = (Equal.rewrite e (x => match Bool x { true => Empty false => Unit }) (Unit.new)) Empty.absurd emp To_beq_nat_true (Nat.succ n1) (Nat.succ n2) e = Equal.apply (x => Nat.succ x) (Extract_equal n1 n2 e) Fro_beq_nat_true (n1: Nat) (n2: Nat) (e: Equal n1 n2) : Equal (Nat.equal n1 n2) Bool.true Fro_beq_nat_true Nat.zero Nat.zero Equal.refl = Equal.refl Fro_beq_nat_true Nat.zero (Nat.succ n2) e = let emp = (Equal.rewrite e (x => match Nat x { zero => Unit succ => Empty }) (Unit.new)) Empty.absurd emp Fro_beq_nat_true (Nat.succ n1) Nat.zero e = let emp = (Equal.rewrite e (x => match Nat x { zero => Empty succ => Unit }) (Unit.new)) Empty.absurd emp Fro_beq_nat_true (Nat.succ n1) (Nat.succ n2) e = let e2 = Succ_n1_n2 n1 n2 e let ind = Fro_beq_nat_true n1 n2 e2 ind Succ_n1_n2 (n1: Nat) (n2: Nat) (e : (Equal Nat (Nat.succ n1) (Nat.succ n2))) : Equal Nat n1 n2 Succ_n1_n2 Nat.zero Nat.zero e = Equal.refl Succ_n1_n2 (Nat.succ n1) Nat.zero e = Equal.apply (x => Nat.pred x) e Succ_n1_n2 Nat.zero (Nat.succ n2) e = Equal.apply (x => Nat.pred x) e Succ_n1_n2 (Nat.succ n1) (Nat.succ n2) e = Equal.apply (x => Nat.pred x) e Extract_equal (n1: Nat) (n2: Nat) (e: Equal (Nat.equal n1 n2) Bool.true) : Equal n1 n2 Extract_equal Nat.zero Nat.zero (Equal.refl) = Equal.refl Extract_equal Nat.zero (Nat.succ n2) (e) = let emp = (Equal.rewrite e (x => match Bool x { true => Empty false => Unit }) (Unit.new)) Empty.absurd emp Extract_equal (Nat.succ n1) Nat.zero (e) = let emp = (Equal.rewrite e (x => match Bool x { true => Empty false => Unit }) (Unit.new)) Empty.absurd emp Extract_equal (Nat.succ n1) (Nat.succ n2) e = Equal.apply (x => Nat.succ x) (Extract_equal n1 n2 e) }
However, while the boolean and propositional formulations of a statement are equivalent from a purely logical point of view, they need not be operationally equivalent. Equality provides an extreme example: knowing that n = m = True is usually of little direct help in the middle of a proof involving n and m; however, if we convert the statement to the equivalent form n = m, we can rewrite it.
The case of even numbers is also interesting. Recall that, when proving the inverse direction of even_bool_prop (i.e., evenb_double, going from the propositional assertion to the boolean one), we used a simple induction on k. On the other hand, the converse (the evenb_double_conv exercise) required some clever generalization, since we cannot directly prove (k => Equal n (Nat.double k)) = Bool.true
For these examples, the propositional assertions are more useful than their boolean counterparts, but this is not always the case. For example, we cannot test whether a general proposition is true or not in a function definition; as a consequence, the following code snippet is rejected:
#![allow(unused)] fn main() { Is_even_prime : Nat -> Bool Is_even_prime = (n: Nat) => Bool.if (Equal n 2n) Bool.true Bool.false }
Kind complains that n = 2 has type Type, while it expects an element of Bool (or some other inductive type with two elements). The reason for this error message has to do with the computational nature of the core language of Kind, which is designed such that every function it can express is computable and total. One reason for this is to allow for the extraction of executable programs from Kind developments. As a consequence, in Kind, Type does not have a universal case analysis operation that says whether a given proposition is true or false, since such an operation would allow for the writing of non-computable functions.
Although non-computable general properties cannot be formulated as boolean computations, it is worth noting that many computable properties are easier to express using Type than Bool, since recursive function definitions are subject to significant restrictions in Kind. For example, the next chapter shows how to define the property that a regular expression matches a given string using Type. Doing the same with Bool would be equivalent to writing a regular expression checker, which would be more complicated, harder to understand, and harder to reason about.
On the other hand, an important additional benefit of stating facts using booleans is enabling some proof automation through computation with terms in Kind, a technique known as reflection proof. Consider the following statement:
#![allow(unused)] fn main() { Even_1000 : Sigma Nat (k => Equal 1000n (Nat.double k)) }
"The most straightforward proof of this fact is to provide the value of k explicitly."
#![allow(unused)] fn main() { Even_1000 = $ 500n Equal.refl }
On the other hand, the proof of the corresponding boolean statement is even simpler:
#![allow(unused)] fn main() { Even_1000a : Equal (Evenb 1000n) Bool.true Even_1000a = Equal.refl }
"Interestingly, as the two notions are equivalent, we can use the boolean formulation to prove the other without explicitly mentioning the value 500."
#![allow(unused)] fn main() { Even_1000b : Sigma Nat (k => Equal 1000n (Nat.double k)) Even_1000b = Sigma.new 500n Equal.refl }
Although we haven't gained much in terms of proof size in this case, larger proofs can be considerably simplified by using reflection. As an extreme example, the proof of the four-color theorem in Coq uses reflection to reduce the analysis of hundreds of different cases to a boolean computation. We won't delve into reflection in great detail, but it serves as a good example that shows the complementary strengths of booleans and general propositions.
Logical_connectives
The following lemmas relate the propositional connectives studied in this chapter to their corresponding boolean operations.
#![allow(unused)] fn main() { Andb_true_equiv (b1: Bool) (b2: Bool) : Equivalence (Equal (Bool.and b1 b2) Bool.true) (Pair (Equal b1 Bool.true) (Equal b2 Bool.true)) Andb_true_equiv b1 b2 = ? Orb_true_equiv (b1: Bool) (b2: Bool): Equivalence (Equal (Bool.or b1 b2) Bool.true) (Either (Equal b1 Bool.true) (Equal b2 Bool.true)) Orb_true_equiv b1 b2 = ? }
Beq_nat_false_equiv
The following theorem is an alternative "negative" formulation of beq_nat_true_equiv that is more convenient in certain situations (we will see examples in later chapters).
#![allow(unused)] fn main() { Beq_nat_false_equiv (n1: Nat) (n2: Nat) : Equivalence (Equal (Nat.equal n1 n2) Bool.false) (Not (Equal n1 n2)) Beq_nat_false_equiv n1 n2 = ? }
Beq_list
Given a boolean operator beq to test the equality of elements of some type a, we can define a function beq_list beq to test the equality of lists with elements in a. Complete the definition of the function beq_list below. To ensure that your definition is correct, prove the theorem beq_list_true_equiv.
#![allow(unused)] fn main() { Beq_list <a> (beq: a -> a -> Bool) (xs: List a) (ys: List a) : Bool Beq_list a beq xs ys = ? Beq_list_true_equiv <a> (beq: a -> a -> Bool) (a1: a) (a2: a) (e: Equivalence (Equal (beq a1 a2) Bool.true) (Equal a1 a2)) (xs: List a) (ys: List a): Equivalence (Equal (Beq_list beq xs ys) Bool.true) (Equal xs ys) Beq_list_true_equiv a beq a1 a2 e xs ys = ? }
All_forallb
#![allow(unused)] fn main() { Forallb <x> (t: x -> Bool) (xs: List x) : Bool Forallb x t List.nil = Bool.true Forallb x t (List.cons xs.h xs.t) = Bool.and (t xs.h) (Forallb t xs.t) }
Prove the theorem below, which relates forallb to the property All from the above exercise.
#![allow(unused)] fn main() { Forallb_true_equiv <x> (t: x -> Bool) (xs: List x) : Equivalence (Equal (Forallb t xs) Bool.true) ((All ((k: x) => Equal (t k) Bool.true) xs)) Forallb_true_equiv x t xs = ? }
Are there any important properties of the function forallb that are not captured by this specification?
Classical vs. Constructive Logic
We have seen that it is not possible to test whether a proposition p is true or not by defining a Kind function. You may be surprised to find out that a similar restriction applies to proofs! In other words, the following principle of intuitive reasoning is not derivable in Kind:
#![allow(unused)] fn main() { Excluded_middle <p>: Either p (Not p) }
To understand operationally why this is the case, recall that to prove a statement of the form Either p q, we use the pattern matches Left and Right, which require knowing which side of the disjunction is true. But the universally quantified proposition p in Excluded_middle is an arbitrary proposition about which we know nothing. We do not have enough information to choose which of Left or Right to apply, just as Kind does not have enough information to mechanically decide whether p is true or not within a function.
However, if we know that p is reflected in some Boolean term b, determining whether it is true or not is trivial: we just check the value of b.
#![allow(unused)] fn main() { Restricted_excluded_middle <p> <q> (b: Bool)(e: Equivalence p (Equal b Bool.true)) : Either p (Not p) Restricted_excluded_middle p q Bool.true (Equivalence.new pb bp) = Either.left (bp Equal.refl) Restricted_excluded_middle p q Bool.false (Equivalence.new pb bp) = Either.right (Empty.absurd (Not_implies_our_not pb)) }
In particular, the third excluded is valid for equations n = m, between natural numbers n and m.
#![allow(unused)] fn main() { Restricted_excluded_middle_eq (n: Nat) (m: Nat) : Either (Equal n m) (Not (Equal n m)) Restricted_excluded_middle_eq n m = ? To_reme (n: Nat) (m: Nat) (e: Equal n m) : Equal (Nat.equal n m) Bool.true To_reme Nat.zero Nat.zero e = Equal.refl To_reme Nat.zero (Nat.succ m) e = Empty.absurd (Not_implies_our_not e) To_reme (Nat.succ n) Nat.zero e = Empty.absurd (Not_implies_our_not e) To_reme (Nat.succ n) (Nat.succ m) e = To_reme n m (Succ_injective n m e) From_reme (n: Nat) (m: Nat) (e: Equal (Nat.equal n m) Bool.true) : Equal n m From_reme Nat.zero Nat.zero e = Equal.refl From_reme Nat.zero (Nat.succ m) e = Empty.absurd (Not_implies_our_not e) From_reme (Nat.succ n) Nat.zero e = Empty.absurd (Not_implies_our_not e) From_reme (Nat.succ n) (Nat.succ m) e = Equal.apply (x => Nat.succ x) (From_reme n m e) }
It may seem strange that the principle of the excluded middle is not available by default in Kind; after all, any assertion must be true or false. However, there is an advantage in not assuming the principle of the excluded middle: statements in Kind can make stronger claims than the analogous statements in standard mathematics. Notably, if there is a proof in Kind of (Sigma a (x => (p x))), we can explicitly exhibit a value of x for which we can prove p x — in other words, every proof of existence is necessarily constructive. Logics like Kind, which do not assume the principle of the excluded middle, are referred to as constructive logics. More conventional logical systems, such as ZFC, in which the principle of the excluded middle is valid for arbitrary propositions, are referred to as classical.
The following example illustrates why assuming the principle of the excluded middle can lead to non-constructive proofs:
Statement: There are irrational numbers a and b, such that a^b is rational.
Proof: It is not difficult to show that the square root of 2 is irrational. If square root of 2 ^ square root of 2 is rational, we can simply take a = b = square root of 2, and we are done .Otherwise, if square root of 2 ^ square root of 2 is irrational, we can take a = square root of 2 ^ square root of 2 and b = square root of 2, since a ^ b = square root of 2 ^ (square root of 2 * square root of 2) = square root of 2 ^ 2 = 2.
Did you notice what happened here? We used the principle of the excluded middle to separately consider the cases where square root of 2 ^ square root of 2 is rational and where it is not, without knowing which one is true! Because of this, we know that such a and b exist, but we cannot determine their actual values (at least, using this line of argument).
As useful as constructive logic is, it has its limitations: there are many statements that can be easily proven in classical logic but have much more complicated constructive proofs, and there are some for which no constructive proof is known! Fortunately, just like the functional extensionality, the principle of the excluded middle is known to be compatible with Kind logic, allowing us to safely add it as an axiom. However, we will not need to do this in this book: the results we cover can be developed entirely within constructive logic at a negligible extra cost.
It takes some practice to understand which proof techniques should be avoided in constructive reasoning, but arguments by contradiction, in particular, are infamous for leading to non-constructive proofs. Here's a typical example: suppose we want to show that there exists an x with some property p, i.e., such that p x. We start by assuming that our conclusion is false; that is Not (Sigma a (x => (p x))). From this premise, it is not difficult to deduce (x: a) -> Not (p x). If we can show that this intermediate fact leads to a contradiction, we arrive at a proof of existence without ever exhibiting a value of x for which p x is true!
The technical failure here, from a constructive standpoint, is that we claim to prove Sigma a (x => (p x)) using a proof o Not (Not (Sigma a (x =>(p x)))). Allowing us to remove double negations from arbitrary statements is equivalent to assuming the excluded middle, as shown in one of the exercises below. Thus, this line of reasoning cannot be encoded in Kind without assuming additional axioms.
Excluded_middle_irrefutable
The consistency of Kind with the general axiom of the excluded middle requires complicated reasoning that cannot be carried out within Kind itself. However, the following theorem implies that it is always safe to assume a decidability axiom (i.e., an instance of the excluded middle) for any specific type p. Why? Because we cannot prove the negation of such an axiom; if we could, we would have both Not (Either p (Not p)) and Not (Not (Either p (Not p))), which is a contradiction.
#![allow(unused)] fn main() { Excluded_middle_irrefutable <p> : Not (Not (Either p (Not p))) Excluded_middle_irrefutable p = ? }
Not_exists_dist
It is a theorem of classical logic that the following two statements are equivalent:
#![allow(unused)] fn main() { Not (Sigma a (k => Not (p k)))) (x : a) -> p x }
The dist_not_exists theorem above proves one side of this equivalence. Interestingly, the other direction cannot be proven in constructive logic. Your task is to show that it is implied by the excluded middle.
#![allow(unused)] fn main() { Not_exists_dist <a> (p: a -> Type) (s: Not (Sigma a (k => Not (p k)))) : (x: a) -> p x Not_exists_dist a p s = ? }
where
#![allow(unused)] fn main() { Excluded_middle <p>: Either p (Not p) // Excluded_middle p = Confia }
Classical_axioms
For those who like a challenge, here's an exercise taken from the book Coq'Art by Bertot and Casteran (p. 123). Each of the following four statements, together with excluded_middle, can be regarded as characterizing classical logic. We cannot prove any of them in Kind, but we can consistently add any one of them as an axiom if we want to work in classical logic.
Prove that all five propositions (these four plus excluded_middle) are equivalent.
#![allow(unused)] fn main() { Peirce <p> <q>(pq: (p -> q) -> p) : p Double_negation_elimination <p> (np: Not (Not p)) : p De_morgan_not_not <p> <q> (np: Pair (Not p) (Not q)) : Either p q Implies_to_or <p> <q> (pq: p -> q) : Either (Not p) q }
Inductively Defined Propositions
In the Logic chapter, we examined various ways of writing propositions, including conjunction, disjunction, and quantifiers. In this chapter, we add a new tool to the mix: inductive definitions.
Remember that we saw two ways to state that a number n is even: we can say (1) Evenb n = Bool.true or (2) (k => Equal n (Nat.double k)). Another possibility is to say that n is even if we can establish its parity based on the following rules:
- Ev_0 Rule: The number
0is even. - Ev_SS Rule: If
nis even, thenNat.succ (Nat.succ n)is even.
To illustrate how this definition of parity works, let's imagine using it to show that 4 is even. By the Ev_SS rule, it suffices to show that 2 is even. This, in turn, is guaranteed again by the Ev_SS rule, provided we can show that 0 is even. But this last fact follows directly from the Ev_0 rule.
We will see many definitions like this throughout the rest of the course. For informal discussions, it is helpful to have a lightweight notation that makes reading and writing easier. Inference rules are one such notation:
$$ \frac{ }{Ev\ \ 0} \ \ ev_0 $$
$$ \frac{\ \ \ \ ev\ \ \ \ \ }{Ev\ \ (Nat.succ \ (Nat.succ \ n))} \ \ ev_SS $$
Each of the textual rules above is reformatted here as an inference rule; the intended reading is that if the premises above the line are all valid, then the conclusion below the line follows. For example, the ev_SS rule says that if n satisfies ev, then Nat.succ (Nat.succ n) also satisfies it. If a rule has no premises above the line, then its conclusion is valid unconditionally.
We can represent a proof using these rules by combining the applications of rules into a proof tree. Here is how we could transcribe the above proof that 4 is even:
$$ \frac{ }{Ev\ \ 0} \ \ ev_0 \ \ \ \ \frac{ }{Ev\ \ 2} \ \ ev_SS \ \ \ \ \frac{ }{Ev\ \ 4} \ \ ev_SS \ \ \ \ \frac{ }{Ev\ \ 6} \ \ ev_SS \ $$
Why call this a "tree" (instead of a "stack," for example)? Because, in general, inference rules can have multiple premises. We will see examples of this below.
Putting it all together, we can translate the definition of parity into a formal definition in Kind using a data declaration, where each constructor corresponds to an inference rule:
type Ev ~ (n: Nat){
ev_0 : Ev Nat.zero
ev_ss <n : Nat> (pred: Ev n) : Ev (Nat.succ (Nat.succ n))
}This definition differs in a crucial aspect from previous uses of data: its result is not a Type but rather a function from Nat to Type – that is, a property of numbers. Note that we have seen other inductive definitions that result in functions, such as List, whose type is Type -> Type. What is new here is that, since the Nat argument of Ev is unnamed and appears to the right of the colon, it is allowed to take different values in the types of different constructors: Nat.zero in the type of ev_z and Nat.succ (Nat.succ n) in the type of ev_ss.
On the other hand, the definition of List globally names the parameter x, forcing the result of Nil and Cons to be the same (List x). If we had tried to omit the type n: Nat when defining ev_ss, we would have seen an error
type Wrong_ev ~ (n: Nat){
wrong_ev_0 : Ev Nat.zero
wrong_ev_ss (pred: Ev n) : Ev (Nat.succ (Nat.succ n))
}With the following return:
- ERROR Cannot find the definition 'n'.
┌──[ev.kind2:9:25]
│
8 │ wrong_ev_z : Ev Nat.zero
9 │ wrong_ev_ss (pred: Ev n) : Ev (Nat.succ (Nat.succ n))
│ ┬ ┬
│ │ └Here!
│ └Here!
10 │
("Parameter" here is jargon from Kind for an argument to the left of the colon in an inductive definition; "index" is used to refer to arguments to the right of the colon.)
We can think of the definition of Ev as defining a property of the Kind Ev: Nat -> Type, along with the theorems ev_z: Ev 0 and ev_ss <n : Nat> (pred: Ev n) : Ev (Nat.succ (Nat.succ n)). Such "constructor theorems" have the same status as proven theorems. In particular, we can apply rule names as functions to each other to prove Ev for specific numbers...
Ev_4 : Ev 4n
Ev_4 = Ev.ev_ss 2n (Ev.ev_ss 0n Ev.ev_z)We can also prove theorems that have hypotheses involving Ev.
Ev_plus5 (n: Nat) : Ev n -> Ev (Nat.add 4n n)
Ev_plus5 n = x => Ev.ev_ss (Ev.ev_ss x)More generally, we can show that any number multiplied by 2 is even.
Ev_double
Ev_double (n: Nat) : Ev (Nat.double n)
Ev_double n = ?Using Evidence in Proofs
In addition to constructing evidence that numbers are even, we can also reason about such evidence. Introducing Ev with a data statement tells Kind not only that the constructors ev_z and ev_ss are valid ways to construct evidence that a number is even, but also that these two constructors are the only ways to construct evidence that numbers are even (in the sense of Ev).
In other words, if someone gives us evidence and claims it to be of the form Ev n, then we know that e must have one of two forms:
eisev_z(and n is Nat.zero), oreisev_ssapplied to induction withnand it is equal to the successor of the successor ofn*.
We've already used this strategy before, remember the Problems.t3 exercise from the induction chapter, here the difference is that there's only one more "Nat.succ" in our induction
This suggests that it should be possible to analyze a hypothesis of the form Ev n in the same way we do with data structures defined inductively; in particular, it should be possible to argue by induction and case analysis on this evidence. Let's see some examples to understand what this means in practice.
Pattern Matching on Evidence
Suppose we are proving some fact involving a number n and we are given the hypothesis Ev n. We already know how to perform case analysis on n using the inversion tactic, generating separate subgoals for the case where n = Nat.zero and the case where n = Nat.succ n for some n. But for some proofs, we may want to directly analyze the evidence that Ev n is true.
By the definition of Ev, there are two cases to consider:
- If the evidence is of the form
ev_z, we know thatn = Nat.zero. - Otherwise, the evidence must have the form
ev_ss n e, wheren = Nat.succ (Nat.succ n)andeis the evidence forEv n.
We can reason about this kind of pattern matching in Kind, again using pattern matching. In addition to allowing us to reason about equalities involving constructors, inversion provides a principle of case analysis for propositions defined inductively.
Ev_minus2 (n: Nat) (e: Ev n) : Ev (Nat.pred (Nat.pred n))
Ev_minus2 Nat.zero e = e
Ev_minus2 (Nat.succ Nat.zero) e = Ev.ev_z
Ev_minus2 (Nat.succ (Nat.succ n)) (Ev.ev_ss e) = eIn words, here is how the pattern matching reasoning works in this proof:
- If the evidence is of the form
ev_z, we know thatn = Nat.zero. Therefore, it is sufficient to show thatEv (Nat.pred (Nat.pred Nat.zero))is valid. By the definition ofNat.pred, this is equivalent to showing thatEv Zis valid, which follows directly fromev_0. - Otherwise, the evidence must have the form
ev_ss n e, wheren = Nat.succ (Nat.succ n)andeis the evidence forEv n. We must then show thatEv (Nat.pred (Nat.pred (Nat.succ (Nat.succ n))))is valid, which, after simplification, follows directly frome.
Evss_ev (n: Nat) (e: Ev (Nat.succ (Nat.succ n))) : Ev nIntuitively, we know that the evidence for the hypothesis cannot consist solely of the constructor ev_z, since Nat.zero and Nat.succ are different constructors of the type Nat; therefore, ev_ss is the only applicable case. Unfortunately, pattern matching is not smart enough to realize this and still generates two subgoals. Even worse, by doing so, it leaves the final goal unchanged, failing to provide any useful information to complete the proof.
The inversion tactic, on the other hand, can detect (1) that the first case does not apply and (2) that the n appearing in the Ev_SS case must be the same as n. This allows us to conclude the proof.
Evss_ev n (Ev.ev_ss e) = e Using dependent pattern matching, we can also apply the principle of explosion to "obviously contradictory" hypotheses involving inductive properties. For example:
One_not_even : Not (Ev 1n)
Inversion_practice
Prove the following results using pattern matching.
Ssssev__even (n: Data.Nat) (e: Ev (Data.Nat.succ (Data.Nat.succ (Data.Nat.succ (Data.Nat.succ n))))) : Ev n
Ssssev__even n e = ?
Even5_nonsense (e: Ev 5n) : Prop.Equal (Data.Nat.add 2n 2n) 9n
Even5_nonsense e = ?The way we use inversion here may seem a bit mysterious at first. So far, we have only used inversion on equality propositions to make use of the injectivity of constructors or to discriminate between different constructors. But we see here that inversion can also be applied to analyze evidence of inductively defined propositions.
Here is how inversion works in general. Suppose the name I refers to an assumption P in the current context, where P was defined by an Inductive statement. Then, for each of the constructors of P, inversion of I generates a subgoal in which I has been replaced by the exact and specific conditions under which this constructor could have been used to prove P. Some of these subgoals will be self-contradictory; inversion discards those. The ones that are left represent the cases that must be proven to establish the original goal. For these, inversion adds all the equations to the proof context that must hold true for the arguments supplied to P (e.g., Nat.succ (Nat.succ k) = n in the proof of evSS_ev).
The exercise ev_double above shows that our new notion of evenness is implied by the two previous ones (since, by even_bool_prop in the Logic chapter, we already know they are equivalent to each other). To show that the three coincide, we just need the following lemma:
Ev_even
(n: Nat)
(e: Ev n) :
(Sigma Nat (k => Prop.Equal n (Nat.double k)))
Ev_even n e = ?We proceed by case analysis on Ev n. The first case can be resolved trivially.
Ev_even Nat.zero e = Sigma.new 0n Equal.reflUnfortunately, the second case is more challenging. We need to show [k: Nat] -> (Equal (Nat.succ (Nat.succ n')) (Nat.double k)), but the only assumption available is e', which states that Ev n' is true. Since this is not directly useful, it seems like we are stuck and that the case analysis on Ev n was a waste of time.
Ev_even (Nat.succ Nat.zero) e = Empty.absurd _ //todoIf we take a closer look at our second goal, however, we can see that something interesting happened: by performing case analysis on Ev n, we were able to reduce the original result to a similar one that involves a different evidence for Ev n: e'. More formally, we can conclude our proof by showing that
Ev_even (Nat.succ (Nat.succ n)) (Ev.ev_ss e) = Ev_even_ss n (Ev_even n e)which is the same as the original statement, but with n' instead of n. In fact, it is not difficult to convince Kind that this intermediate result is sufficient.
Ev_even (Nat.succ (Nat.succ n)) (Ev.ev_ss e) = Ev_even_ss n (Ev_even n e)Induction on Evidence
If this seems familiar, it's no coincidence: we encountered similar problems in the Induction chapter when trying to use case analysis to prove results that required induction. And once again, the solution is... induction!
Let's try our current lemma again:
Ev_even
(n: Nat)
(e: Ev n) :
(Sigma Nat(k => Equal n ( Nat.double k)))
Ev_even Nat.zero e = Sigma.new 0n Equal.refl
Ev_even (Nat.succ Nat.zero) e = Empty.absurd _
Ev_even (Nat.succ (Nat.succ n)) (Ev.ev_ss e) = Ev_even_ss n (Ev_even n e)
// Ev_even (Nat.succ (Nat.succ n)) Ev.ev_z = Caso impossívelThe equivalence between the second and third definitions of evenness now follows.
Ev_even_equiv (n: Nat) : Equivalence (Ev n) (Sigma Nat (k => Equal n (Nat.double k)))
Ev_even_equiv n = Equivalence.new (x => Ev_even n x) (y => From_eee n y)
From_eee (n: Nat) (s: Sigma Nat (k => Equal n (Nat.double k))) : Ev n
From_eee n (Sigma.new a b fst snd) =
Equal.rewrite (Equal.mirror (specialize b into #0 in snd)) (x =>(Ev x)) (Ev_double fst)
Ev_double (n: Nat) : Ev (Nat.double n)
Ev_double Nat.zero = Ev.ev_z
Ev_double (Nat.succ n) = Ev.ev_ss (Ev_double n)
As we will see in the upcoming chapters, induction on evidence is a recurring technique in various areas, especially in the formalization of programming language semantics, where many properties of interest are defined inductively.
The following exercises provide simple examples of this technique to help you become familiar with it.
Ev_sum
Ev_sum (n: Nat) (m: Nat) (e1: Ev n) (e2: Ev m) : Ev (Nat.add n m)
Ev_sum n m e1 e2 = ?
Ev_alternate
In general, there can be multiple ways to define a property inductively. For example, here is an alternative (somewhat forced) definition for Ev:
type Evn ~ (n: Nat){
z : Evn Nat.zero
d : Evn (Nat.succ (Nat.succ Nat.zero))
sum <n : Nat> <m: Nat> (evn: Evn n) (evm: Evn m) : Evn (Nat.add n m)
} Prove that this definition is logically equivalent to the old one. (You may want to refer to the previous theorem when you reach the induction step.)
Ev_evn (n: Nat): Equivalence (Ev n) (Evn n)
Ev_evn n = ?
Ev_ev__ev
Finding the appropriate thing to induct on is a bit tricky here:
Ev_ev_ev (n: Nat) (m: Nat) (e: Ev (Nat.add n m)) (en: Ev n) : Ev m
Ev_ev_ev Nat.zero m e en = ?Ev_plus_plus
This exercise only requires the application of existing lemmas. No induction or even case analysis is needed, although some of the rewrites may be tedious.
Ev_pp
<n: Nat>
<m: Nat>
<p: Nat>
(e1: Ev (Nat.add n m))
(e2: Ev (Nat.add n p))
: Ev (Nat.add m p)
Ev_pp Nat.zero m p e1 e2 =
``Inductive Relations
A proposition parameterized by a number (like Ev) can be considered as a property, meaning it defines a subset of Nat, specifically those numbers for which the proposition holds. Similarly, a proposition with two arguments can be considered as a relation, meaning it defines a set of pairs for which the proposition holds.
A useful example is the "less than or equal" relation between numbers. The following definition should be quite intuitive. It states that there are two ways to provide evidence that a number is less than or equal to another: observe that they are the same number or provide evidence that the first is less than or equal to the predecessor of the second.
type Le (n: Nat) ~ (m: Nat) {
n : Le n n
S <m: Nat> (pred: (Le n m)) : (Le n (Nat.succ m))
}Proofs of facts about Le using the constructors n and S follow the same patterns as proofs about properties, like Ev above. We can apply the constructors to prove goals about Le (e.g., show that Le 3n 3n or Le 3n 6n) and we can use pattern matching to extract information from Le hypotheses in the context (e.g., prove that (Le 2n 1n) -> (Equal (Plus 2n 2n) 5n)).
Here are some sanity checks about the definition. (Note that while they are of the same type as "simple tests" we gave for the test functions we wrote in the early lectures, we must construct their proofs explicitly - Refl doesn't do the job because the proofs are not just a matter of simplifying computations.)
Test_le1 : Le 3n 3n
Test_le1 = Le.n 3n
Test_le2 : Le 3n 6n
Test_le2 = Le.S (Le.S (Le.S Le.n))
Test_le3 (l: Le 2n 1n) : Equal (Nat.add 2n 2n) 5n
Test_le3 Le.n = Empty.absurd // TODO
Test_le3 (Le.S Le.n) = Empty.absurd // TODO
Test_le3 (Le.S (Le.S len)) = Empty.absurd // TODOThe "strictly less than" relation n < m can now be defined in terms of Le.
Lt (n: Nat) (m: Nat) : Type
Lt n m = Le (Nat.succ n) m
Here are some other simple relationships about numbers
type Square_of ~ (n: Nat) (m: Nat) {
sq <n: Nat> : Square_of n (Mult n n)
}
type Next_Nat ~ (n: Nat) (m: Nat) {
Nn <n: Nat> : Next_Nat n (Nat.succ n)
}
type Next_even ~ (n: Nat) (m: Nat) {
1 <n: Nat> (pred: Ev (Nat.succ n)) : Next_even n (Nat.succ n)
2 <n: Nat> (pred: Ev (Nat.succ (Nat.succ n))) : Next_even n (Nat.succ (Nat.succ n))
}
Total_relation (Optional)
Define an inductive binary relation Total_relation that holds for all pairs of natural numbers.
// TODO
Empty_relation (Optional)
Define an inductive binary relation Empty_relation (about numbers) that never holds.
// TODO
Le_exercises (Optional)
Here are some facts about the relations Le and Lt that we will need later in the course. The proofs are good practice exercises.
Le.trans (n: Nat) (m: Nat) (o: Nat) (x: Le m n) (y: Le n o) : Le m o
Le.trans n m o x y = ?
O_le_n (n: Nat) : Le Nat.zero n
O_le_n n = ?
N_le_m_sn_le_sm (n: Nat) (m: Nat) (l: Le n m) : Le (Nat.succ n) (Nat.succ m)
N_le_m_sn_le_sm n m l = ?
Sn_le_Sm_n_le_m (n: Nat) (m: Nat) (l: Le (Nat.succ n) (Nat.succ m)) : Le n m
Sn_le_Sm_n_le_m n m l = ?
Le_plus_l (a: Nat) (b: Nat) : Le a (Nat.add a b)
Le_plus_l a b = ?
Plus_lt (n1: Nat) (n2: Nat) (m: Nat) (lt: Lt (Nat.add n1 n2) m) : Pair (Lt n1 m) (Lt n2 m)
Plus_lt n1 n2 m lt = ?
Lt_S (n: Nat) (m: Nat) (l: Lt n m) : (Lt n (Nat.succ m))
Lt_S n m l = ?
Lte_complete (n: Nat) (m: Nat) (e: Equal (Nat.lte n m) Bool.true) : (Le n m)
Lte_complete n m e = ? Hint: The next one may be easier to prove by induction on m.
Lte_correct (n: Nat) (m: Nat) (le: Le n m) : Equal Bool (Nat.lte n m) Bool.true
Lte_correct n m le = ?Hint: This theorem can be easily proved without using induction.
Lte_true_trans (n: Nat) (m: Nat) (o: Nat)
(l: Equal (Nat.lte n m) Bool.true)
(k: Equal (Nat.lte m o) Bool.true)
: Equal (Nat.lte n o) Bool.true
Lte_true_trans n m o l k = ?lte_iff
Lte_iff (n: Nat) (m: Nat) : Iff (Equal (Nat.lte n m) Bool.true) (Le n m)
Lte_iff n m = ?R_provability
We can define three-place relations, four-place relations, etc., in just the same way as binary relations.
For example, consider the following three-place relation on numbers:
type R ~ (a: Nat) (b: Nat) (c: Nat) {
C1 : R 0n 0n 0n
C2 <m: Nat> <n: Nat> <o: Nat>
(r: R m n o)
: R (Nat.succ m) n (Nat.succ o)
C3 <m: Nat> <n: Nat> <o: Nat>
(r: R m n o)
: R m (Nat.succ n) (Nat.succ o)
C4 <m: Nat> <n: Nat> <o: Nat>
(r: R (Nat.succ m) (Nat.succ n) (Nat.succ (Nat.succ o)))
C5 <m: Nat> <n: Nat> <o: Nat>
(r: R m n o)
}Which of the following propositions are provable?
- R 1n 1n 2n
// TODO
- R 2n 2n 6n
// TODO
- If we dropped constructor C5 from the definition of R, would the set of provable propositions change? Briefly (1 sentence) explain your answer.
// TODO
- If we dropped constructor C4 from the definition of R, would the set of provable propositions change? Briefly (1 sentence) explain your answer.
// TODO
R_fact (Optional)
The relation R above actually encodes a familiar function. Figure out which function; then state and prove this equivalence in Kind
F_R (m: Nat) (n: Nat) : Nat
F_R m n = ?
R_equiv_fR (m: Nat) (n: Nat) (o: Nat) : Iff (R m n o) (Equal (F_R m n) o)
R_equiv_fR m n o = ?Subseq
A list is a subsequence of another list if all the elements of the first list occur in the same order in the second list, possibly with some extra elements between them. For example, [1n,2n,3n] is a subsequence of each of the lists [1n,2n,3n], [1n,1n,1n,2n,2n,3n], [1n,2n,7n,3n], [5n,6n,1n,9n,9n,2n,7n,3n,8n], but it is not a subsequence of any of the lists [1n,2n], [1n,3n], [5n,6n,2n,1n,7n,3n,8n].
Define an inductive type Subseq in List Nat that captures the meaning of being a subsequence. (Hint: You will need three cases.)
- Prove subseq_refl, that subsequence is reflexive, meaning any list is a subsequence of itself.
- Prove subseq_app, that for any lists l1, l2, and l3, if l1 is a subsequence of l2, then l1 is also a subsequence of (App l2 l3).
- (Optional, more challenging) Prove subseq_trans, that subsequence is transitive - meaning if l1 is a subsequence of l2 and l2 is a subsequence of l3, then l1 is a subsequence of l3. Hint: Choose your induction carefully!
R_provability2 (Optional)
Assuming we have given the following definition to Kind:
type Rp ~ (n: Nat) (l: List Nat) {
C1
: Rp 0n []
C2 <n: Nat> <l: List Nat>
(r: Rp n l)
: Rp (Nat.succ n) (List.cons n l)
C3 <n: Nat> <l: List Nat>
(r: Rp (Nat.succ n) l)
}- Rp 2n [1n,0n]
- Rp 1n [1n,2n,1n,0n]
- Rp 6n [3n,2n,1n,0n]
Case Study: Regular Expressions
The property Ev provides a simple example to illustrate inductive definitions and the basic techniques for reasoning about them, but it's not very exciting - after all, it's equivalent to the two non-inductive definitions of parity we've already seen, and it doesn't seem to offer any concrete benefits over them. To give a better sense of the power of inductive definitions, let's show how to use them to model a classic concept from computer science: regular expressions.
Regular expressions are a simple language for describing strings, defined as follows:
type Regexp (t: Type) {
emptyset
emptystr
chr (h: t)
app (st1: Regexp t) (st2: Regexp t)
union (st1: Regexp t) (st2: Regexp t)
star (st1: Regexp t)
}Note that this definition is polymorphic: regular expressions in Reg_exp t describe strings with characters drawn from t - that is, lists of elements of t.
(We deviate slightly from standard practice by not requiring the type t to be finite. This results in a slightly different theory of regular expressions, but the difference is not significant for our purposes.)
We connect regular expressions and strings through the following rules, which define when a regular expression matches a given string:
• The EmptySet expression does not match any string. • The EmptyStr expression matches the empty string []. • The Chr x expression matches the single-character string [x]. • If re1 matches s1 and re2 matches s2, then (App re1 re2) matches (App s1 s2). • If at least one of the expressions re1 and re2 matches s, then Union re1 re2 matches s. • Finally, if we can write a string s as the concatenation of a sequence of strings s = (App s_1 (App... s_k...)), and the expression re matches each of the strings s_i, then Star re matches s.
As a special case, the sequence of strings may be empty, so Star re always matches the empty string [] regardless of what re is.
We can easily translate this informal definition into a data definition as follows:
type Expmatch <t> ~(xs: Data.List t) (r: Regexp t) {
mempty : Expmatch t [] Regexp.emptystr
mchar (x: t) : Expmatch t [x] (Regexp.chr x)
mapp
<s1: Data.List t>
<s2: Data.List t>
<re1: Regexp t>
<re2: Regexp t>
(e1: Expmatch t s1 re1)
(e2: Expmatch t s2 re2)
: Expmatch t (Data.List.concat t s1 s2) (Regexp.app re1 re2)
munionl <s1: Data.List t> (re1: Regexp t) (re2: Regexp t)
(e1: Expmatch t s1 re1)
: Expmatch t s1 (Regexp.union re1 re2)
munionr (re1: Regexp t) <s2: Data.List t> (re2: Regexp t)
(e1: Expmatch t s2 re2)
: Expmatch t s2 (Regexp.union re1 re2)
mstarz (r: Regexp t) : Expmatch t [] (Regexp.star r)
mstarapp
<s1: Data.List t>
<s2: Data.List t>
<r1: Regexp t>
(e1: Expmatch s1 r1)
(e2: Expmatch s2 (Regexp.star r1))
: Expmatch t (Data.List.concat t s1 s2) (Regexp.star r1)
}Let's illustrate these rules with some examples.
Regexp_ex1 : Expmatch [1] (Regexp.chr 1)
Regexp_ex1 = Expmatch.mchar 1
Regexp_ex2 : Expmatch [1, 2] (Regexp.app (Regexp.chr 1) (Regexp.chr 2))
Regexp_ex2 = Expmatch.mapp [1] (Regexp.chr 1) (Expmatch.mchar 1) [2] (Regexp.chr 2) (Expmatch.mchar 2)
Using pattern matching, we can also show that certain strings do not match a regular expression:
Regexp_ex3 : Not (Expmatch [1, 2] (Regexp.chr 1))
Regexp_ex3 = Empty.absurd _We can define auxiliary functions to help write regular expressions. The reg_exp_of_list function constructs a regular expression that matches exactly the list it receives as an argument:
Regexp_of_list <t> (xs: List t) : Regexp t
Regexp_of_list t List.nil = Regexp.emptystr
Regexp_of_list t (List.cons xs.h xs.t) = Regexp.app (Regexp.chr xs.h) (Regexp_of_list t xs.t)
Regexp_ex4 : Expmatch [1, 2, 3] (Regexp_of_list [1, 2, 3])
Regexp_ex4 =
(Expmatch.mapp
[1]
(Regexp.chr 1)
(Expmatch.mchar 1)
[2, 3]
(Regexp_of_list [2, 3])
(Expmatch.mapp
[2]
(Regexp.chr 2)
(Expmatch.mchar 2)
[3]
(Regexp_of_list [3])
(Expmatch.mapp
[3]
(Regexp.chr 3)
(Expmatch.mchar 3)
[]
(Regexp_of_list [])
(Expmatch.mempty)
)
)
)
We can also prove general facts about Exp_match. For example, the following lemma shows that every string s that matches re also matches Star re.
Mstar1 <t> <s: List t> <re: Regexp t> (e: Expmatch s re) : Expmatch s (Regexp.star re)
Mstar1 t s re e =
let msz = Expmatch.mstarz re
let mss = Expmatch.mstarapp s [] re e msz
let lst = List_concat s
let rwt = Equal.rewrite lst (x => (Expmatch t x (Regexp.star re))) mss
rwt
(Note the use of appendNilRightNeutral*** to change the goal of the theorem to exactly the same form expected by MStarApp.)
Exp_match_ex1
The following lemmas show that the informal matching rules provided at the beginning of the chapter can be derived from the formal inductive definition.
Munion
<t>
<s: List t>
<re1: Regexp t>
<re2: Regexp t>
(p: Pair (Expmatch s re1) (Expmatch s re2))
: Expmatch s (Regexp.union re1 re2)
Munion t s re1 re2 (Pair.new fst snd) =
Expmatch.munionl t s [] re1 re2The next lemma is stated in terms of the fold function from the Poly chapter: If ss: List (List t) represents a sequence of strings s1, ..., sn, then fold (++) ss [] is the result of concatenating all of them.
Fold <x> <y> (f: x -> y -> y) (l: Data.List x) (b: y) : y
Fold x y f Data.List.nil b = b
Fold x y f (Data.List.cons xs.h xs.t) b = f xs.h (Fold f xs.t b)
MStar_ <t>
(ss : Data.List (Data.List t))
(re : Regexp t)
(construct_match : (s : Data.List t) -> (i : In s ss) -> Expmatch s re)
: Expmatch (Concats ss) (Regexp.star re)
MStar_ ss re construct_match = ?Reg_exp_of_list
Prove that reg_exp_of_list satisfies the following specification:
Reg_exp_of_list_spec <t> (s1: Data.List t) (s2: Data.List t) : Iff (Expmatch s1 (Regexp_of_list s2)) (Prop.Equal s1 s2)
Reg_exp_of_list_spec s1 s2 = ?Since the definition of Exp_match has a recursive structure, it is expected that proofs involving regular expressions often require induction based on evidence. For example, suppose we wanted to prove the following intuitive result: if a regular expression re matches some string s, then every element of s must occur somewhere in re. To state this theorem, we first define a function re_chars that lists all characters occurring in a regular expression:
Re_chars <t> (re: Regexp t) : Data.List t
Re_chars t Regexp.emptyset = []
Re_chars t Regexp.emptystr = []
Re_chars t (Regexp.chr x) = [x]
Re_chars t (Regexp.app r0 r1) = Data.List.concat (Re_chars r0) (Re_chars r1)
Re_chars t (Regexp.union r0 r1) = Data.List.concat (Re_chars r0) (Re_chars r1)
Re_chars t (Regexp.star r0) = Re_chars r0
Re_star <t> (re: Regexp t) : Prop.Equal (Re_chars (Regexp.star re)) (Re_chars re)
Re_star e re = Prop.Equal.reflWe can then formulate our theorem as follows:
Destruct <a> (x: a) (lx: Data.List a) (ly: Data.List a) (i: In x (Data.List.concat a lx ly)) : (Data.Either (In x lx) (In x ly))
Destruct a x lx ly i =
let Data.Pair.new fst snd = (In_app_iff x lx ly)
let f = (fst :: (_) -> (_)) i
f
Construct <a> (x: a) (lx: Regexp a) (ly: Regexp a) (e: Data.Either (In x (Re_chars lx)) (In x (Re_chars ly))) : In x (Data.List.concat (Re_chars lx) (Re_chars ly))
Construct a x lx ly e = (Data.Pair.snd ( In_app_iff x (Re_chars lx) (Re_chars ly)) :: (_) -> (_)) e
In_re_match <a> (x: a) (re: Regexp a) (s: Data.List a) (e: Expmatch s re) (i: In x s) : In x (Re_chars re)
In_re_match a x (Regexp.emptyset) Data.List.nil e i = i
In_re_match a x (Regexp.emptyset) (Data.List.cons head tail) e i = Data.Empty.absurd _ //todo
In_re_match a x (Regexp.emptystr) (Data.List.nil) Expmatch.mempty i = i
In_re_match a x (Regexp.chr u s) (Data.List.cons t re (Data.List.nil _)) (Expmatch.mchar c) i =
let e0 = Prop.Equal.refl :: Prop.Equal c re
let e1 = Prop.Equal.refl :: Prop.Equal s c
let chn = Prop.Equal.chain e1 e0
let rrt = Prop.Equal.rewrite (Prop.Equal.mirror chn) (y => (Data.Either (Prop.Equal _ x y) _)) i
rrt
In_re_match a x (Regexp.app t z y) (Data.List.concat u l1 l2) e i =
let e0 = Prop.Equal.refl :: Prop.Equal u a
let l3 = l1 :: Data.List a
let l4 = l2 :: Data.List a
let e1 = Prop.Equal.refl :: Prop.Equal l1 l3
let e2 = Prop.Equal.refl :: Prop.Equal l2 l4
let e3 = Prop.Equal.refl :: Prop.Equal (Data.List.concat u l1 l2) (Data.List.concat a l3 l4)
let i = i :: (In a x (Data.List.concat u l1 l2))
let rrt = Prop.Equal.rewrite e3 ((k: (Data.List a))=> (In a x k)) i
let des = Destruct x l3 l4 rrt
des
In_re_match a x re Data.List.nil (Expmatch.mstarz z) i = Data.Empty.absurd _ //todoRe_not_empty
Write a recursive function re_not_empty that tests whether a regular expression matches any string. Prove that your function is correct.
Re_not_empty <t> (re: Regexp t) : Data.Bool
Re_not_empty t re = ?
Re_not_empty_correct <t> <re: Regexp t>
: Equivalence (Data.Sigma (Data.List t) (s => Expmatch s re)) (Prop.Equal (Re_not_empty re) Data.Bool.true)
Re_not_empty_correct t re = ?
The remember Tactic
Rewriting the section, dependent pattern matching solves all of this.
A potentially confusing feature of the induction tactic is that it easily allows you to attempt setting up an induction on a term that is not sufficiently general. The effect of this is to lose information (just as destruct can do) and leave you unable to conclude the proof. Here's an example:
Star_app <a> (re: Regexp a) (s1: Data.List a) (s2: Data.List a) (exp0: Expmatch a s1 (Regexp.star re)) (exp1: Expmatch a s2 (Regexp.star re))
: (Expmatch (Data.List.concat s1 s2) (Regexp.star re))
Star_app a re (Data.List.nil _) s2 (Expmatch.mstarz e) exp1 = exp1
Star_app a re s1 s2 (Expmatch.mstarapp t r s r1 m ms) exp1 =
let e0 = Prop.Equal.refl :: Prop.Equal r1 re
let e1 = Prop.Equal.refl :: Prop.Equal (Data.List.concat r s) s1
let ind = Expmatch.mstarapp m (Star_app r1 s s2 ms exp1)
let rrt = Prop.Equal.rewrite e0 (x => (Expmatch _ _ (Regexp.star _ x))) ind
let aux = App_assoc r s s2
let rrt = Prop.Equal.rewrite aux (x => (Expmatch _ (x) (_))) rrt
let rrt = Prop.Equal.rewrite e1 (x => (Expmatch t (Data.List.concat _ x s2) (Regexp.star t re))) rrt
rrtExp_match_ex2
MStar2 <t> (re: Regexp t) (s: Data.List t) (ss: Data.List (Data.List t)) (exp: Expmatch s (Regexp.star re))
: (Data.Pair (Prop.Equal s (Fold (x => y => Data.List.concat x y ) ss [])) ((s2: Data.List t) -> (In s2 ss) -> (Expmatch s2 re)))The lemma MStar'' below (along with its inverse, the exercise MStar' above), shows that our definition of Exp_match for Star is equivalent to the one informally given earlier.
pumping
One of the earliest truly interesting theorems in the theory of regular expressions is the so-called pumping lemma, which states, informally, that any sufficiently long string s matching a regular expression re can be "pumped" by repeating some middle section of s an arbitrary number of times to produce a new string also matching re.
To start, we need to define what it means to be "sufficiently long". Since we are working in a constructive logic, we actually need to be able to compute, for each regular expression re, the minimum length for strings s to guarantee "pumpability".
pumping_constant :Next, it is useful to define an auxiliary function that repeats a string (appends itself) a certain number of times.
napp :
Now, the pumping lemma itself states that if s => re and if the length of s is at leas't the pumping constant of re, then s can be divided into three substrings s1 ++ s2 ++ s3 such that s2 can be repeated any' number of times, and the result, when combined with s1 and s3, will still match re. Since D is also guaranteed to be non-empty, this gives us a (constructive!) way of generating strings matching re that are as long as we desire.
pumping :To speed up the proof (which you should fill in), the omega tactic, which is enabled by the Require below, is helpful in several places to automatically complete tedious low-level arguments involving equalities or inequalities over natural numbers. We will revisit the omega tactic in a later chapter, but feel free to try it now if you'd like. The first case of the induction gives an example of how it is used.
pumping m le = ?pumping_rhsCase Study: Improving Reflection
In the Logic chapter, we saw that we often need to relate Boolean computations to Type statements. However, performing this conversion as we did there can result in tedious proof scripts. Consider the proof of the following theorem:
filter_not_empty_In : {n : Nat} -> Not (filter ((==) n) l = []) -> In n l //terminarIn the second case, we explicitly apply the beq_nat_true lemma to the equation generated when doing a dependent match on n == x, to convert the assumption n == x = Bool.true into n = m.`
We can simplify this by defining an inductive proposition that provides a better case analysis principle for n == m. Instead of generating an equation like n == m = Bool.true, which is often not directly useful, this principle immediately gives us the assumption we actually need: n = m.
In fact, we will define something slightly more general, which can be used with arbitrary properties (not just equalities):
type Reflect (p: Type) (b: Bool) { //TODO: corrigir
ReflectT (p: Type) (b = True) : Reflect p b
ReflectF (p: Type) (n: Not p) (b = False) : Reflect p b
}The "reflect" property takes two arguments: a proposition p and a Boolean b. Intuitively, it states that the property p is reflected in (i.e., equivalent to) the Boolean b: p is true if and only if b = Bool.true. To understand this, note that by definition, the only way to obtain evidence that "Reflect p True" is true is by showing that p is true and using the "ReflectT" constructor. If we reverse this statement, it means that it should be possible to extract evidence for p from a proof of "Reflect p True". Similarly, the only way to show "Reflect p False" is by combining evidence of "Not p" with the "ReflectF" constructor.
It is easy to formalize this intuition and show that the two statements are indeed equivalent:
Equiv_reflect <b: Bool> (e: Equiv p (b = True)) : Reflect p b
Equiv_reflect Bool.false (pb, _) = ReflectF (uninhabited . pb) Equal.refl
Equiv_reflect Bool.true (_, bp) = ReflectT (bp Refl) Equal.reflReflect_equiv
Reflect_equiv (r: Reflect p b) : Equivalence p (Bool.equal b Bool.true)
Reflect_equiv x = ?The advantage of "Reflect" over the usual "if and only if" connective is that when we destruct a hypothesis or lemma of the form "Reflect p b", we can perform a case analysis on b while simultaneously generating appropriate hypotheses in both branches (p in the first subgoal and Not p in the second).
Beq_natP <n: Nat> <m : Nat> : Reflect (Equal n m) (Nat.equal n m)
Beq_natP {n} {m} = iff_reflect (iff_sym (beq_nat_true_iff n m))The new proof of filter_not_empty_In now proceeds as follows. Notice how the calls to destruct and apply are combined into a single destruct call.
(To see this clearly, compare the two proofs of filter_not_empty_In with Kind and observe the differences in the proof state at the beginning of the first case of destruct.)
Filter_not_empty_In_ <n : Nat> <n: Not (filter ((x => y => Nat.equal x y) n) l = []) : In n lBeq_natP_practice
Use beq_natP, as mentioned above, to prove the following:
Count (n : Nat) : (l : List Nat) : Nat
Count n List.nil = 0n
Count n (List.cons xs.h xs.t) = Nat.add (Bool.if (Nat.equal n xs.h) 1n 0n) (Count n xs.t)
Beq_natP_practice (e: Equal (count n l) Nat.zero) : Not (In n l)
Beq_natP_practice e = ? Indeed, this technique provides us with only a small convenience advantage for the proofs we have seen here, but using "Reflect" consistently often results in noticeably shorter and clearer proof scripts as the proofs grow larger. We will see many more examples in the upcoming chapters.
The use of the "reflect" property was popularized by SSReflect, a Coq library that has been used to formalize important results in mathematics, including the Four Color Theorem and the Feit-Thompson Theorem. The name SSReflect stands for "small-scale reflection," which refers to the widespread use of reflection to simplify small proof steps involving Boolean computations.
Additional Exercises
Nostutter
Formulating inductive definitions of properties is an important skill that you will need in this course. Try to solve this exercise without any help.
We say that a list "stutters" if it repeats the same element consecutively. The property "Nostutter my_list" means that my_list does not stutter. Formulate an inductive definition for Nostutter. (This is different from the NoDup property in the exercise below; the sequence [1,4,1] repeats but does not stutter.)
type Nostutter <t> (l: List t) {
RemoveMe : Nostutter []
}Make sure each of these tests passes, but feel free to change the suggested proof (in comments) if it does not work for you. Your definition may be different from ours and still be correct; in that case, the examples may need a different proof. (You will notice that the suggested proofs use various tactics we have not discussed to make them more robust against the different possible ways of defining Nostutter. You can probably just uncomment them and use them as is, but you can also prove each example with more basic tactics.)
Test_nostutter_1 : Nostutter [3n,1n,4n,1n,5n,6n]
Test_nostutter_1 = ?
// Prova. repita o construtor; aplique beq_nat_false_iff; auto.
Test_nostutter_2 : Nostutter []
Test_nostutter_2 = ?
// Prova. repita o construtor; aplique beq_nat_false_iff; auto.
Test_nostutter_3 : Nostutter [5n]
Test_nostutter_3 = ?
// Prova. repita o construtor; aplique beq_nat_false; auto. Qed.
Test_nostutter_4 : Not (Nostutter [3n,1n,1n,4n])
Test_nostutter_4 = ?
// Prova. intro.
// repetir correspondência de metas com
// h: nostutter _ |- _ => inversão h; limpar h; subst
// end.
// contradição H1; auto.Filter_challenge
Let's prove that our definition of filter from the Poly chapter corresponds to an abstract specification. Here is the specification, informally written in English:
A list l is an "ordered merge" of l1 and l2 if it contains all the same elements as l1 and l2, in the same order as l1 and l2, but possibly interleaved. For example,
[1n,4n,6n,2n,3n] is an ordered merge of [1n,6n,2n] and [4n,3n].
Now, suppose we have a set t, a function test: t -> Bool, and a list l of type List t. Suppose further that l is an ordered merge of two lists, l1 and l2, such that every item in l1 satisfies test and no item in l2 satisfies test. Then, filter test l = l1.
Translate this specification into a theorem in Kind and prove it. (You will need to start by defining what it means for a list to be an ordered merge of two lists. Do this with an inductive data type, not a function.)
Filter_challenge_2
A different way to characterize the behavior of filter is as follows: Among all the subsequences of l that have the property that test evaluates to True for all their elements, filter test l is the longest one. Formalize this statement and prove it.
Palindromes
A palindrome is a sequence that reads the same forwards and backwards.
-
Define an inductive proposition Pal about List t that captures what it means to be a palindrome. (Hint: You will need three cases. Your definition should be based on the structure of the list; having just a single constructor like
C <t> (l : List t) (rev: Equal l (Rev l)) : Pal lmay seem obvious, but it won't work very well.)
-
Prove (pal_app_rev) that
(l : List t) : Pal (List.concat l (Rev l)) -
Prove (pal_rev) that
(l : List t) (p: Pal l) : Equal l (Rev l)
Palindrome_converse
Again, the reverse direction is significantly harder, due to the lack of evidence. Using your definition of Pal from the previous exercise, prove that
(l : List t) ( Equal l (Rev l)) Pal lNoDup
Remember the definition of the In property from the Logic chapter, which states that a value x appears at least once in a list l:
In <t> (x : t) (l : List t) : Type
In x List.nil = Empty
In x (List.concat xs.h xs.t) = Either (Equal x xs.h) (In x xs)Your first task is to use In to define an inductive proposition Disjoint <t> l1 l2, which should be provable exactly when l1 and l2 are lists (with elements of type t) that have no elements in common.
Next, use In to define an inductive proposition NoDup <t> l, which should be provable exactly when l is a list (with elements of type t) in which every member is different from all the others. For example, NoDup U60 [1,2,3,4] and NoDup Bool [] should be provable, while NoDup Nat [1n,2n,1n] and NoDup Bool [Bool.true,Bool.true] should not.
Finally, state and prove one or more interesting theorems that relate Disjoint, NoDup, and List.
Pigeonhole principle
The pigeonhole principle states a basic fact about counting: if we distribute more than n items into n pigeonholes, some pigeonhole must contain at least two items. As often happens, this seemingly trivial fact about numbers requires nontrivial machinery to prove, but now we have enough... First, prove an easy and useful lemma.
In_split
<t>
<x: t>
<l: List t>
(i: In x l)
: ([l1] -> [l2] -> ((Equal l (List.concat l1 (List.cons x l2)))))
In_split i = ?Now define a property Repeats in such a way that Repeats <t> l asserts that l contains at least one repeated element (of type t).
type Repeats <t> (l: List t) {
// PREENCHA AQUI
RemoveMe' : Repeats [] // necessário para verificação de tipo, os dados não devem estar vazios
}This proof is much easier if you use the excluded_middle hypothesis to show that In is decidable, i.e., Either (In x l) (Not (In x l)). However, it is also possible to do the proof without assuming that In is decidable; if you can do that, you won't need the excluded_middle hypothesis.
Here is one way to formalize the pigeonhole principle. Suppose the list l2 represents a list of pigeonhole labels, and the list l1 represents the labels assigned to a list of items. If there are more items than labels, at least two items must have the same label—i.e., the list l1 must contain repetitions.
Pigeonhole_principle <t> (x: t)
(l1: Data.List t)
(l2: Data.List t)
(i1: In x l1)
(i2: In x l2)
(lt: Lt (Data.List.length l1) (Data.List.length l2))
: Repeats l1
Pigeonhole_principle t x l1 l2 i2 i2 lt = ?
Excluded_middle : (p : Type) : Either p (Not p)