Number Lists

Generalizing the definition of pairs, we can describe the type of number lists as follows: "A list is either the empty list or a set of one element and another list", this type is not composed of a head and a tail.

type List (t) {
  nil
  cons (head: t) (tail: List t)
}

As we are dealing with only one type, it is interesting to rewrite the list type for a defined one, the chosen one was Nat:

type NatList {
  nil
  cons (head: Nat) (tail: NatList)
}

or

type NatList {
   List Nat
}

We can see that in both notations, there is a head and a tail, with the head receiving an element of type Nat and the tail receiving a list of type Nat.

For example, a list of three natural numbers 1n, 2n, and 3n would be written as follows:

[1n, 2n, 3n]

However, the Kind reads it differently:

[1n, [2n, 3n]]

where 1n is the head and [2n, 3n] is the tail. Likewise, looking at a list of 4 elements [1n, 2n, 3n, 4n], we now see it as follows:

[1n, [2n, [3n, 4n]]]

The list has the head 1n and the tail [2n, [3n, 4n]], which, in turn, has the head 2n and the tail [3n, 4n] which also has its head 3n and its tail 4n.

It may seem scary, but it's a friendly monster:

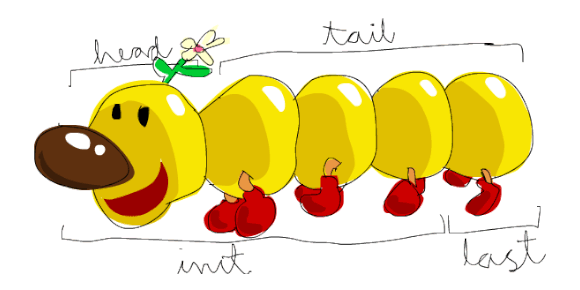
[fonte da imagem: http://learnyouahaskell.com/starting-out]

Repeat

The function repeat takes a number n and a value, returning a list of size n where all elements are the declared value.

// Exemplo: (Repeat 3 Bool.true) -> [True, True, True]
Repeat (x: Nat) (count: Nat) : List Nat
Repeat x Nat.zero            = [] 
Repeat x (Nat.succ count)    = List.cons Nat x (Repeat count x)

Length

The function length calculates the size of the list.

// Exemplo: (Length [1,2,3]) -> 3
Length (xs: List Nat) : Nat
Length List.nil              = 0n
Length (List.cons head tail) = (Nat.succ (Length tail))

Concat

The function concat concatenates (appends) two lists.

Concat (xs: List Nat) (ys: List Nat) : List Nat
Concat (List.nil)            ys = ys
Concat (List.cons head tail) ys = List.cons Nat head (Concat tail ys)

Head and Tail

The head function returns the first element (the "head") of the list, while tail returns everything except the first element (the "tail"). Of course, an empty list has no first element, so we must handle this case with a Maybe type, receiving a Maybe.none if the list is empty or a Maybe.some if it has a value.

// Exemplo: (Head 0n [1n,2n,3n]) -> 1n
Head (default: Nat) (xs: List Nat) :  Nat
Head default (List.nil)            = default
Head default (List.cons head tail) = head

// Exemplo: (Tail Nat [1,2,3]) -> [2,3]
Tail (xs: List Nat)        : List Nat
Tail (List.nil)            = []
Tail (List.cons head tail) = tail

Test_head1 : Equal Nat (Head 0n [1n,2n,3n]) 1n
Test_head1 = Equal.refl

Test_head2 : Equal Nat (Head 0n List.nil) 0n
Test_head2 = Equal.refl

Test_head3 : Equal (List Nat) (Tail [1n, 2n, 3n]) [2n, 3n]
Test_head3 = Equal.refl

Exercises

List_funs

Complete the definitions of Nonzeros, Oddmembers, and Countoddmembers below. Take a look at the tests to understand what these functions should do.

Nonzeros (xs: List Nat) : List Nat
Nonzeros xs = ?

Test_nonzeros : Equal (List Nat) (Nonzeros [0n,1n,0n,2n,3n,0n,0n]) [1n,2n,3n]
Test_nonzeros = ?

Oddmembers (xs: List Nat) : List Nat
Oddmembers xs = ?

Test_oddmembers : Equal (List Nat) (Oddmembers [0n,1n,0n,2n,3n,0n,0n]) [1n,3n]
Test_oddmembers = ?

CountOddMembers (xs: List Nat)  : Nat
CountOddMembers xs = ?

Test_countoddmembers1 : Equal Nat (CountOddMembers [1n,0n,3n,1n,4n,5n]) 4n
Test_countoddmembers1 = ?

Alternate

Complete the definition of alternate, which compacts two lists into one, alternating between elements taken from the first list and elements from the second. See the tests below for more specific examples.

Alternate (xs: List Nat) (ys: List Nat) : List Nat
Alternate xs ys = ?

Test_alternate1 : Equal (List Nat) (Alternate [1n,2n,3n] [4n,5n,6n]) [1n,4n,2n,5n,3n,6n]
Test_alternate1 = ?

Test_alternate2 : Equal (List Nat) (Alternate [1n] [4n,5n,6n]) [1n,4n,5n,6n]
Test_alternate2 = ?

Test_alternate3 : Equal (List Nat) (Alternate  [1n,2n,3n] [4n]) [1n,4n,2n,3n]
Test_alternate3 = ? 

Test_alternate4 : Equal (List Nat) (Alternate [] [20n,30n]) [20n,30n]
Test_alternate4 = ?

Functions

Complete the following definitions for the count, sum, add, and member functions of natural number lists.

Count (v: Nat) (xs: List Nat) : Nat
Count v xs = ?

Test_count1 : Equal Nat (Count 1n [1n,2n,3n,1n,4n,1n]) 3n
Test_count1 = ?

Test_count2 : Equal Nat (Count 6n [1n,2n,3n,1n,4n,1n]) 0n
Test_count2 = ?

Sum (xs: List Nat) (ys: List Nat) : List Nat
Sum xs ys = ?

Test_sum1 : Equal Nat (Count 1n (Sum [1n,2n,3n] [1n,4n,1n])) 3n
Test_sum1 = ?

Add (n: Nat) (xs: List Nat) : List Nat
Add n xs = ?

Test_add1 : Equal Nat (Count 1n (Add 1n [1n,4n,1n])) 3n
Test_add1 = ?

Test_add2 : Equal Nat (Count 5n (Add 1n [1n,4n,1n])) 0n
Test_add2 = ?

Member (v: Nat) (xs: List Nat) : Bool
Member v xs = ?

Test_member1 : Equal Bool (Member 1n [1n,4n,1n]) Bool.true
Test_member1 = ?

Test_member2 : Equal Bool (Member 2n [1n,4n,1n]) Bool.false
Test_member2 = ?

More_functions

Here are some more functions of List Nat for you to practice with. When remove_one is applied to a list without the number to be removed, it should return the same unchanged list.

Remove_one (v: Nat) (xs: List Nat) : List Nat
Remove_one v xs = ?

Test_remove_one1 : Equal Nat (Count 5n (Remove_one 5n [2n,1n,5n,4n,1n])) 0n
Test_remove_one1 = ?

Test_remove_one2 : Equal Nat (Count 5n (Remove_one 5n [2n,1n,4n,1n])) 0n
Test_remove_one2 = ?

Test_remove_one3 : Equal Nat (Count 4n (Remove_one 5n [2n,1n,5n,4n,1n,4n])) 2n
Test_remove_one3 = ?

Test_remove_one4 : Equal Nat (Count 5n (Remove_one 5n [2n,1n,5n,4n,5n,1n,4n])) 1n
Test_remove_one4 = ?

Remove_all (v: Nat) (xs: List Nat) : List Nat
Remove_all v xs = ?

Test_remove_all1  : Equal Nat (Count 5n (Remove_all 5n [2n,1n,5n,4n,1n])) 0n
Test_remove_all1  = ?

Test_remove_all2  : Equal Nat (Count 5n (Remove_all 5n [2n,1n,4n,1n])) 0n
Test_remove_all2  = ?

Test_remove_all3  : Equal Nat (Count 4n (Remove_all 5n [2n,1n,5n,4n,1n,4n])) 2n
Test_remove_all3  = ?

Test_remove_all4  : Equal Nat (Count 5n (Remove_all 5n [2n,1n,5n,4n,5n,1n,4n,5n,1n,4n])) 0n
Test_remove_all4  = ?

Subset (xs: List Nat) (ys: List Nat)  : Bool
Subset xs ys = ?

Test_subset1 : Equal Bool (Subset [1n,2n] [2n,1n,4n,1n]) Bool.true
Test_subset1 = ?

Test_subset2 : Equal Bool (Subset [1n,2n,2n] [2n,1n,4n,1n]) Bool.false
Test_subset2 = ?

Theorem

Write down an interesting theorem involving the count and add functions and prove it. Note that, as this problem is somewhat open-ended, you may come up with a theorem that is true but whose proof requires techniques you have not yet learned. Feel free to ask for help if you get stuck!

Theorem : ?